Suma odległości punktu P od ścian czworościanu maturzystaR: Wewnątrz czworościanu foremnego wybrano dowolny punkt P. Wykaż, że suma odległości punktu P od wszystkich ścian czworościanu jest równa wysokości tego czworościanu.

Adamm: Uogólnij https://pl.wikipedia.org/wiki/Twierdzenie_Vivianiego

Adamm: działa dla dowolnego wymiaru

Adamm: dla dowolnych sympleksów ∑ V_r = V ∑ C_d*P*s_r = C_d*P*h gdzie C_d − stała zależna tylko od wymiaru P − pole (d−1 wymiarowa miara Lebesgue'a) s_r − odległość względem r−tej ściany h − wysokość V_r − r−ta objętość (d wymiarowa miara Lebesgue'a) V − objętość sympleksu stąd od razu ∑_r s_r = h

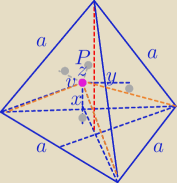
Mila: Odcinki x,y,z,v są prostopadłe do odpowiednich ścian. Dzielisz czworościan na 4 czworościany o wierzchołku P i podstawach , które są odpowiednimi ścianami. Korzystasz z równoważności objętości.

1
	*U{a2√3{4}*H=
3

	1
=		*(U{a2√3{4}*x+U{a2√3{4}*y+U{a2√3{4}*z+U{a2√3{4}*v)⇔
	3

x+y+z+v=H cnw

Mila:

a2√3
	powinno być.
4

Adamm: co to jest "równoważność objętości" ?