Ostrołupy
Master: W ostrosłupie prawidłowym czworokątnym o krawędzi podstawy długości
a = 2 dm kąt między ścianami bocznymi ma miarę 135 stopni
. Ostrosłup ten przecięto dwiema płaszczyznami równoległymi do postawy
na trzy bryły o równych objętościach. Oblicz odległość między tymi
płaszczyznami.
22 gru 19:17
wredulus_pospolitus:
1) rysunek
2) zaznaczenie na rysunku kąta pomiędzy ścianami bocznymi
3) wyznaczenie odległości punktu przy kącie a środka podstawy
4) wyznaczenie odległości pomiędzy tymże punktem a wierzchołkiem podstawy
5) zastosowanie proporcji (podobieństwo trójkątów prostokątnych) w celu wyznaczenia wysokości
6) wyznaczenie ile będą wynosić 'odległości' od wierzchołka do tychże płaszczyzn korzystając z
proporcji i objętości:
V
duży ostrosłup = 3*V
najmniejszy ostrosłup
| | 1 | | 3√9 | |
Pp*H = 3*(x2Px)*(xH) −> x = |
| = |
| |
| | 3√3 | | 3 | |
| | 3√9 | |
więc hnajmniejszego ostrosłupa = |
| H |
| | 3 | |
oblicz tak samo h
średniego ostrosłupa
22 gru 19:49
Master:
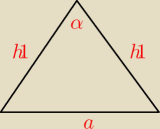
W sumie robiłem podobnie tylko powstało parę problemów.
a=2
√2
α=135
z tw cos
8=2h
12+
√2*h
12
h
1=2*
√2−√2
oznaczam krawędż boczną jako b, krawędź podstawy jako c=2dm i wysokośc sciany bocznej
opadającej na podstawę jako h2
Tw pitagorasa
h
22 +1
2=b
2
Oraz P=1/2*b*h
1 = 1/2*2*h
2 /// *2,()
2
b
2*h
12=4h
22 ==> wstawiajac z tw pitagorasa
(h
22+1)
2*h
12=4h
22
Ale podstawiając za h1 równanie nie ma rozwiązań rzeczywistych i co robię źle?
22 gru 21:14
wredulus_pospolitus:
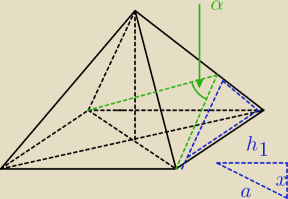
1)
po co
"oznaczam krawędż boczną jako b, krawędź podstawy jako c=2dm i wysokośc sciany bocznej
opadającej na podstawę jako h2
Tw pitagorasa
h
sup>22 +12=b2"
Wystarczy zauważyć 'niebieski' trójkąt prostokątny i wyliczasz 'x' mając 'a' i h1
22 gru 21:21
wredulus_pospolitus:
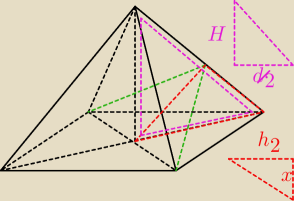
zauważyć podobieństwo czerwonego i fioletowego trójkąta prostokątnego (podobieństwo KKK)
wyliczyć h
2 (wysokość albo z pierwszego (zielonego) trójkąta ... albo z czerwonego
(przeciwprostokątna to połowa przekątnej podstawy) z Pitagorasa
22 gru 21:25
Master: Dobra rozumiem i dziękuję
22 gru 22:11
Master: Choć dalej nie wiem gdzie mam błąd w swoich
22 gru 22:12
wredulus_pospolitus:
więc otrzymujesz:
(h
22 + 1
2)
1*h
12 = 4h
22 (bo przecież podstawiasz za b
2 ... a nie za b
)
h
22(h
12 − 4) = −h
12
h
22( 8 − 4
√2 − 4) = −(8 − 4
√2)
h
22*(4 − 4
√2) = 4
√2 − 8
| | √2 − 2 | | −√2 | |
h22 = |
| = |
| = √2 |
| | 1 − √2 | | −1 | |
h
2 =
4√2
22 gru 22:34