Oblicz ilosc rozwiązań.
Kozak: Ile rozwiązań ma równanie cos5(x) − sin5(x) = 1 w przedziale <−4π, 4π>?
22 gru 16:18
Adamm:
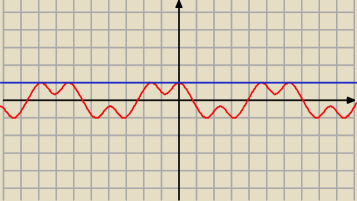
22 gru 18:50
Kozaczek: A bez wykresu ? ?
22 gru 18:53
wredulus_pospolitus:
trywialne rozwiązania:
1) cosx = 1 oraz sinx = 0
2) cosx = 0 oraz sinx = −1
I teraz dla sprawdzamy czy jeszcze gdzieś mogą być rozwiązania:
cos5x − sin5x = 1 ma jakąkolwiek rację bytu tylko jeżeli: cosx ∊ (0;1) i sinx∊(−1;0)
wtedy:
cos5x < cos4x
−sin5x < sin4x
więc:
cos5x − sin5x < cos4x + sin4x = (cos2x + sin2x)(cos2x − sin2x) = cos2x − sin2x =
cos(2x) ≤ 1
22 gru 19:08
wredulus_pospolitus:
więc to są jedyne możliwe przypadki ... dla jakich x ∊ < −4π ; 4π > masz (1) lub (2).
22 gru 19:09
wredulus_pospolitus:
równie dobrze można było ograniczyć:
cos5x < cos2x
−sin5x < sin2x
22 gru 19:11
Kozak: Czyli w sumie tych rozwiązań będzie 8 czy 9?
22 gru 21:26
wredulus_pospolitus:
w przedziale: [0 + 2kπ, 2π + 2kπ) będą dokładnie 2 rozwiązania dla każdego 'k'
Ty masz takich (pełnych) przedziałów dokładnie 4 i jeszcze musisz dorzucić x=4π (w którym także
jest jedno rozwiązanie) ... więc rozwiązań będzie dokładnie:

22 gru 21:31
Kozak: To w sumie 9
22 gru 22:13

