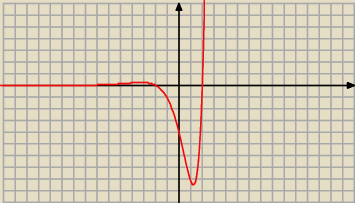
Wyznacz przedziały na których funkcja f (x)=(x^2 - 4)e^x jest rosnąca i wypukła Brad: Wyznacz przedziały na których funkcja f (x)=(x² − 4)e^x jest rosnąca i wypukła jednocześnie

iteRacj@: 1/ czy funkcja f(x) jest różniczkowalna? 2/ jaki warunek musi być spełniony, żeby funkcja różniczkowalna była rosnąca? 3/ jaki warunek musi spełniać funkcja, żeby była wypukła?

Janek191: x* f '(x) = 2 x *e^x + ( x² − 4)*e^x = (x² + 2 x − 4)*e^x x² + 2 x − 4 > 0 Δ = 4 − 4*1*(−4) = 4*5 √Δ = 2√5

	−2 − 2√5
x1 =		= − 0,5 − 0,5 √5
	4

oraz x₂ = −0,5 + 0,5√5 więc f '(x) > 0 ⇔ x ∊ ( − ∞, x₁ ) ∪ ( x₂ ; +∞) Oblicz drugą pochodną. Funkcja jest wypukła dla takich x, że f ' '(x)>0.