pole pod wykresem
Bartu: Witam, mam problem z rozwiązaniem tego zadania. Mógłby ktoś sprawdzić jego poprawność ?
Nie miałem tego poprawnie wytłumaczonego i szukam informacji po internecie.. 1 przykład mi nie
wystarczył żeby to ogarnąć.
https://imgur.com/a/szrosck
20 gru 18:44
wredulus_pospolitus:
nie potrzebnie dzielisz na dwie całki
po prostu:
| | x3 | | 2√x3 | |
∫01 (x2 − (− √x)) dx = [ |
| + |
| ]01 |
| | 3 | | 3 | |
ale sam wynik poprawny
20 gru 18:56
Mila:
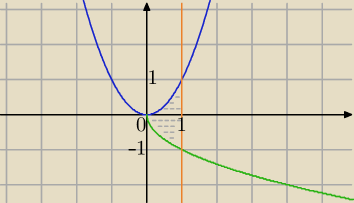
Pole ograniczone krzywymi:
y=x
2, y=−
√x, x=1
P=
0∫
1((x
2−(−
√x)) dx=
0∫
1((x
2+
√x) dx=
| | 1 | | 2 | | 1 | | 2 | |
= |
| *1+ |
| *1−0= |
| + |
| =1 |
| | 3 | | 3 | | 3 | | 3 | |
20 gru 18:57
Jerzy:
Pole obszaru jest symetryczne względem OX.
P = 2*0∫1 x2dx
20 gru 18:58
Jerzy:
Upss... wycofuję mój post
20 gru 18:59
wredulus_pospolitus:
można też by było się 'pobawić' w wyliczenie bez liczenia całki (wyjść z tego, że funkcja
odwrotna y=−√x na przedziale <0;1> to y = −x2 i z tego wykazać, że zakreskowany obszar ma
to samo pole prostokąt o bokach 1 i g(1) gdzie g(x) = x2)
20 gru 19:04
Bartu: Dzięki wam serdeczne !
20 gru 20:16
Mila:
20 gru 21:45