Obliczanie nierówności (kwadratowej), sprawdzanie obliczeń LUKI332: Możecie zobaczyć czy to dobrze zrobiłem, polecenie rozwiąż nierówność : (x−5)²−5|x−5|+6≥0 Założyłem że |x−5|=t, |x−5|²=(x−5)² Czyli : t²−5t+6≥0 Δ=1 x1=2 x2=3 x∊{2,3}={x∊R, (x−5)²−5|x−5|+6≥0} Czy to jest dobrze zrobione ponieważ zaeanje jest na 6 pkt, a tak mało napisałem

PW: No nie, przecież policzyłeś, że t=2 lub t=3, a miałeś policzyć x.

wredulus_pospolitus: a po drugie ... zupełnie nie rozumiem Twojej ostatniej linijki

PW: Prostuję (bo to jest nierówność): policzyłeś, że t≤2 lub t≥3.

LUKI332: Ale teraz jak obliczyć x? Oto jest pytanie

LUKI332: Z tych danych co mam?

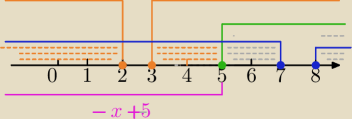
wredulus_pospolitus: z tego co wyliczyłeś to: t∊<0;2> u <3;+∞) |x−5| ∊<0;2> u <3;+∞) (x−5) ∊(−∞ ; −3> u <−2;2> u <3;+∞) x ∊(−∞ ; −3+5> u <−2+5 ; 2+5 > u <3+5;+∞) czyli: x ∊(−∞ ; 2> u < 3 ; 7 > u < 8;+∞)

Mila: 1) Rozwiązałabym standardowo, w przedziałach. |x−5|=x−5 dla x≥5 wtedy mam nierówność: (x−5)²−5(x−5)+6≥0 x²−10x+25−5x+25+6≥0 x²−15x+56≥0 Δ=225−4*56=225−224

	15−1		15+1
x=		lub x=
	2		2

x=7 lub x=8 [x≤7 lub x≥8 ] i x≥5⇔ ∞).html">x∊<5,7>∪<8,∞) 2) |x−5|=−x+5 dla x<5 wtedy mamy nierówność: (x−5)²−5(−x+5)+6≥0 x²−10x+25+5x−25+6≥0 x²−5x+6≥0 x₁=2 lub x₂=3 [x≤2 lub x≥3] i x<5 x≤2 lub x∊<3,5) ============ odp. x∊(−∞,2)∪<3,7>∪<8,∞) ==================

LUKI332: Dziękuję bardzo wam