geom. analityczna
pfdr: Przez punkty A(0,0) B(4,0) C(2,1) przeprowadzić koło (napisać jego równanie), następnie
obliczyć kąt, jaki tworzą ze sobą styczne poprowadzone w punktach A i B.
Czy ktoś mógłby rozwiązać całe to zadanie? Potrafię wyznaczyć równania stycznych, ale wychodzą
zbyt dziwne wyniki, żeby kąt wyszedł bez przybliżenia.
z góry dziękuję!
19 gru 19:54
Mila:
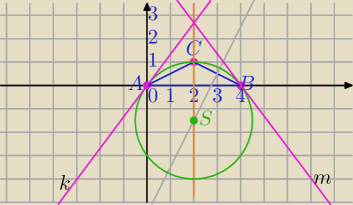
A(0,0) B(4,0) C(2,1)
1) środek okręgu:
Symetralna AB: x=2
Symetralna BC: P(x,y) − punkt symetralnej
(x−4)
2+y
2=(x−2)
2+(y−1)
2
Punkt przecięcia ;
x=2
2) długość promienia:
| | 5 | |
R=|SA|=√22+(3/2)2=√4+(9/4)= |
| |
| | 2 | |
3) Styczne:
k: y=ax+b i A(0,0)∊k⇔b=0
k: y=ax prosta ma jeden punkt wspólny z okręgiem
Równanie okręgu:
| | 9 | | 25 | |
x2−4x+4+a2x2+3ax+ |
| = |
| |
| | 4 | | 4 | |
(1+a
2)x
2+x*(3a−4)=0
x*[(1+a
2)*x+3a−4]=0 równanie ma jedno rozwiązanie x=0 , dla 3a−4=0
===========
m: y=ax+b i B=(4,0) ∊m
a*4+b=0 , b=−4a
m: y=ax−4a⇔ax−y−4a=0
| | 5 | | |a*2+(3/2)−4a| | |
d(S,m)= |
| = |
| |
| | 2 | | √a2+1 | |
stad:
9a
2+24a+16=0 stąd:
=================
α≈73,74
o
==========
19 gru 21:30
Eta:
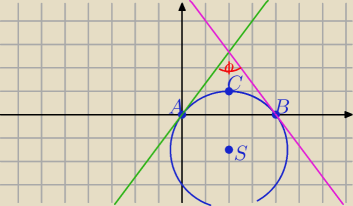
| | 5 | |
o: (x−2)2+(y+32)2=254 S(2,−32) , r= |
| |
| | 2 | |
| | 4 | | 4 | |
styczna w punkcie A : y= |
| x a1= |
| |
| | 3 | | 3 | |
| | 4 | | 16 | | 4 | |
styczna w punkcie B : y= − |
| x+ |
| a2=− |
| |
| | 3 | | 3 | | 3 | |
| | a1−a2 | | 24 | |
tgΦ=| |
| | ⇒tgΦ= |
| ≈3,429 |
| | 1+a1*a2 | | 7 | |
Φ≈74
o
=====
19 gru 22:09
Eta:
Ja styczną wyznaczam tak:
w punkcie A (0,0) (0−2)(x−2)+(0+1,5)(y+1,5)=25/4
styczna w punkcie B(4,0) (4−2)(x−2)+(0+1,5)(y+1,5)=25/4
19 gru 22:13
Mila:
Wiem, ale tego wzoru licealiści nie znają.

19 gru 22:22
Eta:
A szkoda

Ja kiedyś swoim uczniom taki podawałam
19 gru 22:28
Eta:
Inny sposób wyznaczania równania okręgu z postaci ogólnej
Okrąg o: x
2+y
2−2ax−2by+c=0 ( wzór jest w tablicach maturalnych
A(0,0) to c=0
B(4,0) to 16−8a=0 ⇒ a= 2
| | 3 | | 25 | |
C(2,1) to 4+1−8−2b=0 ⇒ b= |
| i r2=a2+b2−c ⇒ r2= |
| |
| | 2 | | 4 | |
S(a,b)
19 gru 22:34
 A(0,0) B(4,0) C(2,1)
1) środek okręgu:
Symetralna AB: x=2
Symetralna BC: P(x,y) − punkt symetralnej
(x−4)2+y2=(x−2)2+(y−1)2
A(0,0) B(4,0) C(2,1)
1) środek okręgu:
Symetralna AB: x=2
Symetralna BC: P(x,y) − punkt symetralnej
(x−4)2+y2=(x−2)2+(y−1)2


 Ja kiedyś swoim uczniom taki podawałam
Ja kiedyś swoim uczniom taki podawałam