Wektory gradientu
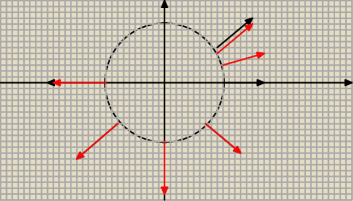
Adamson: Naszkicować wektory gradientu zaczepione w punktach okręgu O = {(x, y) : x2+y2 = 1}
19 gru 19:23
ABC: a gdzie funkcja dla której liczymy gradient?
19 gru 19:37
zdesperowany: f(x,y)=1/4(x2+y2)2
a punkt P =(√2/2,√2/2)
19 gru 19:40
Adamson: o dokładnie! przepraszam
to ta funkcja 1/4...
19 gru 19:46
ABC: no to pochodne cząstkowe po x i po y trzeba policzyć najpierw
19 gru 19:49
zdesperowany: w sumie ten gradient wyszedł taki sam jak ten punkt też te pierwiastki
, tylko gorzej jak miałby wyglądać ten wektor:(
19 gru 19:50
Adamson: gradient w punkcie mam,
wychodzi taki sam jak punkt
ale co dalej?
19 gru 19:52
ABC: zaczepiasz wektor w tym punkcie , jeżeli się nie pomyliłeś, to będzie wektor o długości 1
skierowany pod kątem 45 stopni
19 gru 20:02
zdesperowany: a moźesz to narysować? bo ma być kilka wektorów finalnie...
19 gru 20:24
ABC: a w jakich jeszcze innych punktach?
19 gru 20:30
Adamson: Znaczy i mi sie wydawało że powinien być tylko jeden
nie wiem czemu w zadaniu jest kilka
19 gru 20:30
zdesperowany: no w treści jest naszkicować wektory w punktach okręgu o coś tam na 1 poście jest wzór
19 gru 20:36
ABC:
δf/δx=x(x
2+y
2)
δf/δy=y(x
2+y
2)
i na tym okręgu x
2+y
2=1
czyli w każdym jego punkcie gradient to wektor [x,y]
każda ta strzałka ma długość 1 nie umiem tu rysować
19 gru 20:39
zdesperowany: Dziękuję bardzo bardzooo
19 gru 20:51
Adamson: Dołączam do podziękowań
19 gru 22:37
ABC: 
19 gru 22:41