ostrosłupy atakują ostrosłupik: Podstawa i jedna ze ścian bocznych ostrosłupa są trójkątami równobocznymi, zawierającymi się w płaszczyznach prostopadłych. Oblicz miarę kata między ścianami z których żadna nie jest trójkątem równobocznym.

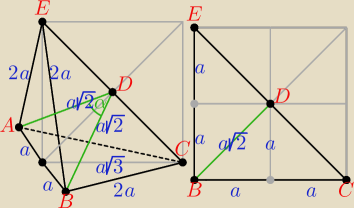
Bogdan: Ściany boczne ostrosłupa: ACE i BCE są trójkątami prostokątnymi. |AB| = 2a, |AD| = |BD| = a√2, |AD|² + |BD|² = |AB|², α = 90^o Trójkąt ABD jest prostokątny.

ostrosłupik: Poprawna odpowiedź to 72^o, więc chyba coś jest nie tak.

Mila: Skąd masz taką odpowiedź?

	1
Ja ma wynik: cosα=		i to jest więcej niż 72o.
	5

Sprawdź odpowiedź, ja sprawdzę obliczenia

Eta: Faktycznie Bogdan zaznaczył ( pomyłkowo)w szarym kwadracie boki o długości 2a a powinien zaznaczyć boki długości a√3

	a√6
wtedy |FD|=		gdzie F to środek odcinka AB
	2

	2
zatem w ΔFBD tg(α/2)=		≈0,8163 ⇒α/2≈ 39o
	√6

to α=78^o ( ale nie 72^o jak podajesz =======

Eta: Jak podała Mila

	1
Z tw. kosinusów cosα=		⇒ α≈78o
	5

an: Eta: Faktycznie Bogdan zaznaczył ( pomyłkowo)w szarym kwadracie boki o długości 2a a powinien zaznaczyć boki długości a√3 Bogdan pisze: "Ściany boczne ostrosłupa: ACE i BCE są trójkątami prostokątnymi" i to jest pomyłka .