Krótkie zadanie z geometrii analitycznej janek: Dany jest trójkąt ABC gdzie A(1,2) B(1,10) C(9,10). Przez punkt D(5,7) poprowadzono prostą o współczynniku kierunkowym dodatnim, która przecina boki AC i BC trójkąta odpowiednio w punktach E i F. Wyznacz współrzędne punktów E i F dla których pole czworokąta AEFB jest największe. Z: a_d>0 prosta AC: y=x+1 prosta BC:y=10 prosta d przechodząca przez punkty E i F: y=ax+b, ale punkt D ∊ d ⇒ 7=5a+b ⇒ b=7−5a prosta d: y=ax+7−5a próbuje wyznaczyć punkt przecięcia z osiami

janek: z prostymi* x+1=ax+7−5a 10=ax+7−5a (−) x=9 y=9a+7−5a y=4a+7

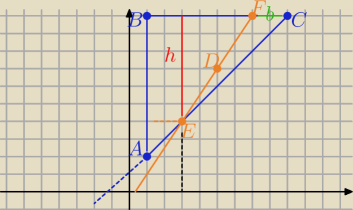
Eta: Zrób rysunek ΔABC połówka kwadratu o boku 8 a>1 z założenia ( bo prosta EF pokrywałaby się z prostą AC

	6−5a		6a−7
E: x+1=ax+7−5a ⇒ x=		to y=
	a−1		a−1

	6−5a		6a−7
E(		,		)
	a−1		a−1

============= Analogicznie F ..... otrzymasz

	5a+3
F(		,10)
	a

========== Pole czworokąta będzie największe wtedy gdy pole ΔEFC będzie najmniejsze Zbadaj minimum pola ΔEFC

	1
P(EFC)=		h*b h= 10−yE , b= 8−xF
	2

i policz P^'(a)=....................... i P^'(a)=0 po uwzględnieniu a>1 otrzymasz a=1,5 podstaw a=1,5 i wyznacz współrzędne punktów E i F Odp: E(3,4), F(7,10) ============

janek: Jak doszedłeś/aś do tego, że y=(6a−7)/(a−1)?

Eta: Widzę chochlika (sorry

	5a−6		5a−6		5a−6+a−1		6a−7
x=		to y= x+1 =		+1=		=
	a−1		a−1		a−1		a−1

Piotrek: Wydaje mi się, że b=9−x_F bo gdy damy 8 pochodna nie będzie równała się 0

Eta: Tak, ma być b=9−x_F ( sorry to literówka