trudne Michał: W równoległoboku ABCD o kącie rozwartym 120⁰ i bokach AB=9 i BC=4 poprowadzono środkową AE boku BC Na boku DC obrano punkt F tak,ze DC=3DF , odcinki AE i BF przecinają się w punkcie M Oblicz pole czworokąta CFME

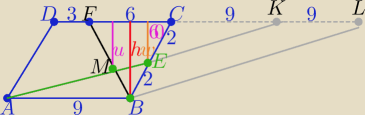
Eta: 1/ rysunek 2/kąt ostry 60^o 3/ dorysujmy odcinki EK ∥ BL 4/ to |KL|=|CK|=|AB|=9 i |FL|=24 i |FK|=15 5/ h=2√3 , w=√3 z podobieństwa trójkątów FBL i FMK z cechy (kkk)

	24		8
w skali k=		=
	15		5

	h		8		5		10√3
to		=		⇒ u=		*2√3=
	u		5		8		8

P(CFME)=P(FMK)−P(CEK)

	1		75√3
P(FMK)=		*15*u =
	2		8

	1		36√3
P(CEK)=		*9*w =
	2		8

	75√3−36√3
to P(CFME)=
	8

	39√3
P(CFME)=		[j2]
	8

≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈ Taką masz odpowiedź?

Mila: Też mam taki wynik, innym sposobem.

Mila: A Michał nie czyta