Dla jakich wartości parametru m równanie ma rozwiązania? Klaudia: Dla jakich wartości parametru m równanie sin ²x + sin x + m = 0 ma rozwiązania? wiem, że podstawiamy t=sinx i t=<−1,1> t²+t+m=0 I Δ=0 II Δ>0 g(1)≥0 − i nie mam pojęcia skąd się to wzięło.. Czy ktoś byłby w stanie wyjaśnić?

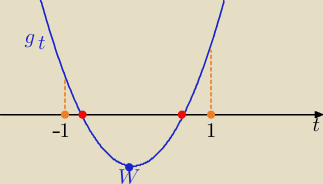
Eta: sinx=t , t∊<−1,1> t²+t+m=0 1/dla Δ=0 1−4m=0 ⇒ m=1/4 2/ dla Δ>0 czyli dla m<1/4 parabola ramionami do góry równanie ma dwa rozwiązania w przedziale t∊<−1,1> to g(−1)≥0 lub g(1)≥0 ⇒ 1−1+m≥0 lub +1+m≥0 ⇒ m≥ −2 i m<1/4 m∊<−2,1/4) i uwzględniając z 1/ m=1/4 Odp: dla m∊<−2,1/4> równanie ma rozwiązania ====================

wredulus_pospolitus: t² + t + m = 0 (t + 0.5)² + (m − 0.25) = 0 z takiej postaci widzimy, że: dla m> 1/4 brak rozwiązań (lewa strona > 0) dla m=1/4 mamy jedno rozwiązanie (t = −0.5) dla m < 1/4 mamy potencjalnie dwa rozwiązania (o ile tylko t ∊ <−1;1> ) i teraz: 1) zauważamy, że x_wierzchołka paraboli NIE ZALEŻY od parametru m (patrz zapisana postać), 2) x_wierzchołka = −0.5 i jest 'bliżej' x=−1 niż x=1 3) w takim razie dla f(−1) ≤ 0 i y_wierzchołka < 0 będziemy mieli dwa rozwiązania ( m ∊ <0 ; 1/4) ) 4) w takim razie dla f(−1) > 0 i f(1) ≤ 0 i y_wierzchołka < 0 będziemy mieli jedno rozwiązanie ( m ∊ <−2 ; 0) )

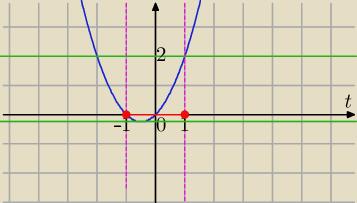
Mila: Graficznie: sin 2x + sin x + m = 0⇔ (*) sin²x+sinx=−m sinx=t , |t|<1 g(t)=t²+t y=−m 1) zbiór wartości g(t) w przedziale <−1,1>:

	−1
tw=
	2

	−1		1		1		1
g(		)=		+(−		)=−		− najmniejsza wartość g(x)
	2		4		2		4

g(1)=2− największa wartość g(t), w przedziale <−1,1> 2) równanie (*) ma rozwiązania dla

	1
−		≤−m≤2 /*(−1)
	4

1
	≥m≥−2
4

	1
m∊<−2,		>
	4

============

student: czemu Mila kopiuje znaki równości od Ety?

Jerzy: Bo w podstawówce siedziały w jednej ławce.

Eta:

Eta: **************************** ^^^^^^^^^^^^^^^^^^^ >>>>>>>>>>>>>>>>>>> <<<<<<<<<<<<<<<<<<< =================== #################### &&&&&&&&&&&&&&&& ~~~~~~~~~~~~~~~~~~~ @@@@@@@@@@@ $$$$$$$$$$$$$$$$$$$$ ♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥ ≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈

Jerzy: Dzięki.Właśnie maluję pokój i zostało mi pier........ć szlaczek

Eta:

Klaudia: Dziękuję wszystkim za pomoc

Eta: