Sporządź rysunek poglądowy do zadania: uuuu: Sporządź rysunek poglądowy do zadania: Znajdź równanie płaszczyzny przechodzącej przez punkt A=(−1,3,2) i prostą

	⎧	x1−x2−x3+3=0
L:	⎩	x1+2x2+x3−5=0

Zadanie potrafie rozwiązać ale mam problem ze sporządzeniem poprawnego rysunku poglądowego.

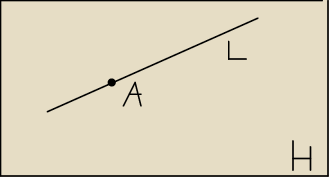
Jan: Moim zdaniem nic innego lepszego tu nie potrzeba

uuuu: Tylko, że punkt A nie należy do prostej L. W takim przypadku wystarczyłoby policzyć z pęku płaszczyzn równanie płaszczyzny przechodzącej jedynie przez prostą L a takich płaszczyzn jest nieskończenie wiele.

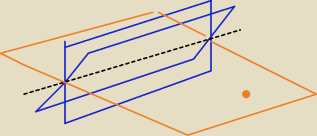
jc: A tak z pęku płaszczyzn wybierasz jedyną płaszczyznę przechodzącą przez A. Czy taki rysunek pasuje?

uuuu: O ten mi się już bardziej podoba. Czy muszę dodatkowo zaznaczać wektory równoległy do prostej L oraz prostopadły do płaszczyzny H, aby rysunek był pełny? Korzystając z równania pęku płaszczyzn powołujemy się również na wektory u ⊥ L i v ⊥ L H: α(u₁x₁+u₂x₂+u₃x₃+u₀)+β(v₁x₁+v₂x₂+v₃x₃+v₀)

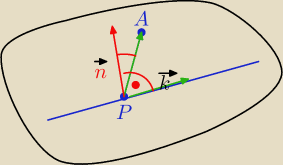
Mila: 1) Znajdujemy punkt należący do prostej L L: x−y−z+3=0 x+2y+z−5=0 ========= + 2x+y=2 dla y=2 mamy x=0, z=1 P=(0,2,1)∊L 2) k^→[1,−1,−1] x [1,2,1] =[1,−2,3] wektor kierunkowy prostej Znajdujemy punkt należący do prostej L 3)A=(−1,3,2) PA^→=[−1,1,1] n^→=AP^→ x k^→=[−1,1,1] x [1,−2,3]=[5,4,1] 4) H: 5*(x+1)+4*(y−3)+z−2=0 5x+4y+z−9=0 =================

jc: Nie zaznaczałby, rysunek stanie się nieczytelny. Poza tym prostopadłość jest z innego świata. O ile α i β nie są równocześnie zerami, mamy płaszczyznę zawierającą tę samą krawędź (bo równość zachodzi dla 2 różnych punktów z krawędzi).

jc: Nie powołujemy się ... Wystarczy, że wiemy, iż ax+by+cz+d=0 opisuje płaszczyznę. To możemy przyjąć za aksjomat, oczywiście (a,b,c)≠(0,0,0).