Jak określić dziedzinę prostej nierówności? KTR: Mam do rozwiązania prostą nierówność

2		1
	<
x+2		x

Wychodzi mi tylko, że x≠−2 i x≠0 oraz x<2 a w odpowiedzi jest jeszcze, że nie ma przedziału (−2,0). Jak udowodnić, że x≠(−2,0)

wredulus_pospolitus: jeżeli x∊(−2,0) to:

2
	> 0
x+2

natomiast

1
	< 0
x

sprzeczne

KTR: OK, co robić gdy nie jest to takie oczywiste? Zawsze się przyrównuje obie strony do zera i patrzy co się dzieje pomiędzy przedziałami zerowymi?

wredulus_pospolitus: emmm ... jeżeli masz f(x) < g(x) i wiesz, że f(x) < 0 dla x∊(−∞ , a) oraz f(x) > 0 dla x∊(a;+∞) oraz, że g(x) < 0 dla x∊(−∞ , b) oraz g(x) > 0 dla x∊(b;+∞) to musisz rozpatrzyć trzy przypadki: 1) x ∊ (−∞, min(a,b)) 2) x ∊ (min(a,b), max(a,b)) 3) x∊ (max(a,b) , + ∞) przy czym drugi przypadek może być sprzeczny tak jak to było w powyższym przypadku

Eta:

2		1
	<		, x≠0 i x≠ −2
x+2		x

2		1
	−		<0
x+2		x

2x−x−2
	<0
x(x+2)

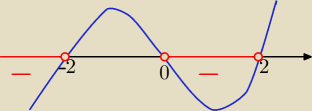
(x−2)*x*(x+2)<0 Odp: x∊(−∞, −2)U (0,2) ================

daras: o i to jest prawidłowa odpowiedź !