pola czworokątów Rolka: W czworokącie wypukłym ABCD odcinki łączące środki przeciwległych boków przecinają się w punkcie O i dzielą czworokąt na cztery czworokąty. Udowodnij, że suma pól każdych dwóch czworokątów, których jedynym punktem wspólnym jest punkt O równa się połowie pola czworokąta ABCD.

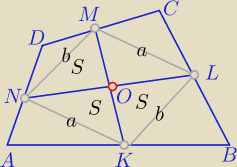
Mila: 1) czworokąt KLMN jest równoległobokiem

	1
|NK|=|ML|=		|BD| ( NK − odcinek łączący środki boków ΔBDA ⇔jest równoległy do BD
	2

i równy połowie BD)

	1
|KL|=|MN|=		|AC|
	2

Przekątne dzielą ten równoległobok na 4 trójkąty o równych polach. 2) Spróbuj dalej sama

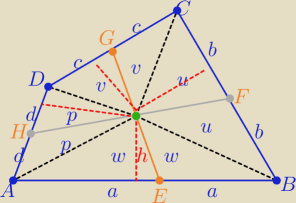
Eta: Pola odpowiednich trójkątów oznaczam : p.w,u,v P(ABCD)= 2p+2w+2u+2v)= 2(p+w+u+v) P(AEOH)+P(FCGO)=P(EBFO)+P(GDHO)=w+u+v+p = 1/2P(ABCD)

Eta: A Rolka .. zaniemówił/a

Rolka: Tak zaniemówiłam , bo jestem pod wrażeniem, nie wiem czy dalej dam radę?

Eta: Wszystko Ci przedstawiłam na rys.

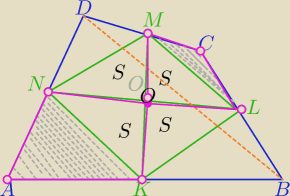
Mila: cd. P_ABCD=P

	1		1
2) PKLMN=4S=		PABCD=		P ⇔
	2		2

	1
S=		P
	8

	1		1
3) ΔAKN∼ΔABD w skali k=		⇔PΔAKN=		PΔABD
	2		4

	1		1
ΔLMC∼ΔDBC w skali k=		⇔PΔLMC=		PΔDBC
	2		4

	1
PAKON=PΔAKN+S=		PΔABD+S
	4

	1
PMOLC=PΔLMC+S=		PΔDBC+S
	4

===================== sumujemy pola tych czworokątów

1		1
	PΔABD+S+		PΔDBC+S=
4		4

	1
=		*(PΔABD+PΔDBC)+2S=
	4

	1		1		1		1
=		*P+2S=		*P+		P=		P
	4		4		4		2

Analogiczne dla drugiej pary czworokątów, dorysować drugą przekątną. Jeśli interesuję Cię ten sposób i masz pytania, to jestem na forum.

Eta:

Eta: @Mila jestem zdziwiona,że nie akceptujesz mojego rozwiązania co daje tezę w 2 minuty i dwie linijki pisania

Mila: Ależ akceptuję, jak najbardziej Uważam, że jest łatwiejszy do zrozumienia dla autorki zadania.. Skończyłam to, co zaczęłam i tyle. Pozdrawiam.

Rolka: Dziękuję Eta i Mila za pomoc.