gffg
TheDanceOfEternity: Naszkicuj wykres funkcji f(x)=√4−4x+x2−2√x2+2x+1. Korzystając z wykresu funkcji f określ
liczbę
rozwiązań równania f(x)=−2x+b w zależności od parametru b.
Więc narysowałem tą funkcję bez problemu, jednak mam kłopot z tym parametrem
−2x+b (a dokładniej to z tym x co tam jest)
14 gru 22:04
TheDanceOfEternity: W dodatku w odpowiedziach jest podany przedział b, dla którego f ma 3 rozwiązania.
Z wykresu nie wynika, że takie rozw. istnieją.
14 gru 22:08
Satan: No to najwidoczniej źle narysowałeś funkcję. Wklep w jakiś kalkulator graficzny, np. Geogebra.
Z rysunku wynika, że istnieje takie b, dla którego są 3 rozwiązania. Między innymi dla b = 0
masz 3 rozwiązania.
14 gru 22:20
Adamm:
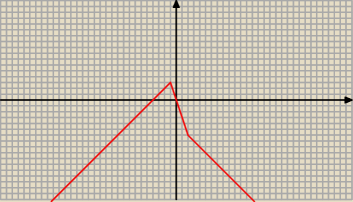
14 gru 22:23
Mila:
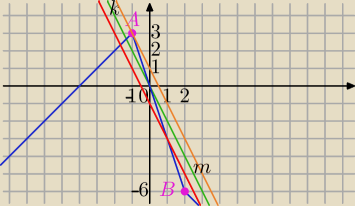
(1) |x−2|−2|x+1|=−2x+b
f(x)=|x−2|−2|x+1|
g(x)=−2x
f(−1)=3, f(2)=−6⇔A=(−1,3), B=(2,−6)
Znaczenie wsp. b
prostą k: y=−2x przesuwamy o wektor [0,b]
1) równanie prostej równoległej do k i przechodzącej przez A=(−1,3)
3=−2*(−1)+b,
b=1
m: y=−2x+1
Równanie (1) ma dwa rozwiązania dla b=1
2) dla b>1 równanie jedno rozwiązanie
3) równanie prostej równoległej do k i przechodzącej przez punkt B=(2,−6)
−6=−2*2+b,
b=−2
n: y=−2x−2
dla b=−2 równanie (1) ma dwa rozwiązania
4) dla
b∊(−2,1) równanie ma 3 rozwiązania
5)
b<−2 jedno rozwiązanie
Uporządkuj informacje i daj odpowiedź.
14 gru 22:36
Mila:

15 gru 16:27

 (1) |x−2|−2|x+1|=−2x+b
f(x)=|x−2|−2|x+1|
g(x)=−2x
f(−1)=3, f(2)=−6⇔A=(−1,3), B=(2,−6)
Znaczenie wsp. b
prostą k: y=−2x przesuwamy o wektor [0,b]
1) równanie prostej równoległej do k i przechodzącej przez A=(−1,3)
3=−2*(−1)+b, b=1
m: y=−2x+1
Równanie (1) ma dwa rozwiązania dla b=1
2) dla b>1 równanie jedno rozwiązanie
3) równanie prostej równoległej do k i przechodzącej przez punkt B=(2,−6)
−6=−2*2+b, b=−2
n: y=−2x−2
dla b=−2 równanie (1) ma dwa rozwiązania
4) dla b∊(−2,1) równanie ma 3 rozwiązania
5) b<−2 jedno rozwiązanie
Uporządkuj informacje i daj odpowiedź.
(1) |x−2|−2|x+1|=−2x+b
f(x)=|x−2|−2|x+1|
g(x)=−2x
f(−1)=3, f(2)=−6⇔A=(−1,3), B=(2,−6)
Znaczenie wsp. b
prostą k: y=−2x przesuwamy o wektor [0,b]
1) równanie prostej równoległej do k i przechodzącej przez A=(−1,3)
3=−2*(−1)+b, b=1
m: y=−2x+1
Równanie (1) ma dwa rozwiązania dla b=1
2) dla b>1 równanie jedno rozwiązanie
3) równanie prostej równoległej do k i przechodzącej przez punkt B=(2,−6)
−6=−2*2+b, b=−2
n: y=−2x−2
dla b=−2 równanie (1) ma dwa rozwiązania
4) dla b∊(−2,1) równanie ma 3 rozwiązania
5) b<−2 jedno rozwiązanie
Uporządkuj informacje i daj odpowiedź.
