zad
matthew: Cześć,
Mam takie zadanie:
Wyznacz wszystkie wartośći parametru p, dla których równanie |x−2| + |x+3| = p ma dokładnie dwa
rozwiązania.
i teraz nie wiem....
czy to ma przyjmować taką postać?
|x−2| + |x+3| = p
x<−2 −2≤x<3 3≥x
−−−−−−−−−|−−−−−−−−−−−|−−−−−−−−−>
x
−2 3
i mam obliczać tak jak równanie z wartościami bezwzględnymi?
Bardzo proszę o pomoc

15 lut 23:53
KK: Potraktuj to jako funkcję i narysuj w układzie współrzędnych. Odczytaj z rysunku, dla których
wartości parametru p równanie ma 2 rozwiązania

16 lut 00:03
Eta:
Nie takie końce tych przedziałów

| |
−−−−−−−(−3)−−−−−−−−−−−−(2)−−−−−−−−
16 lut 00:10
Eta:
Najprościej z wykresów
f(x) : dla x <−3 to f(x) = −x+2−x−3= −2x −1=> f(x)= −2x +1
dla x €<−3,2) f(x)= −x +2 +x +3= 5 => f(x)= 5
dla x€<2,∞) f(x)= x−2+x+3= 2x +1 => f(x)= 2x+1
narysuj ten wykres częśćiami w zadanych przedziałach
wykres y= p musi przecinać wykres f(x) w dwu różnych punktach
więc wyjdzie Ci odp> dla p>5
16 lut 00:15
Eta:
Tak jak podpowiada
KK ..... fajny nick

16 lut 00:17
matthew:
aj faktycznie... zapomniałem o tym...

|x−2| ⇒ x = 2
|x+3| ⇒ x = −3
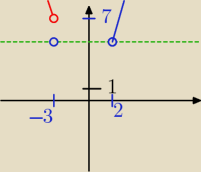
dobra to mam tak:
na zielono: f(x) = 5
na niebiesko f(x) = 2x+1
na czerwono f(x) = −2x + 1
chyba mam źle zrobiony rysunek...
mnie wyszło, że dwa rozwiązania dla p ∊ (7, +
∞)
16 lut 00:32
matthew: może to inicjały

16 lut 00:35
pan tenorek: ide spać. dobranoc

16 lut 00:43
Eta:

dla
p>5
A teraz należy się duuuuuuuuuuuża kawa

16 lut 01:16


 | |
−−−−−−−(−3)−−−−−−−−−−−−(2)−−−−−−−−
| |
−−−−−−−(−3)−−−−−−−−−−−−(2)−−−−−−−−

 aj faktycznie... zapomniałem o tym...
aj faktycznie... zapomniałem o tym...  |x−2| ⇒ x = 2
|x+3| ⇒ x = −3
dobra to mam tak:
na zielono: f(x) = 5
na niebiesko f(x) = 2x+1
na czerwono f(x) = −2x + 1
chyba mam źle zrobiony rysunek...
mnie wyszło, że dwa rozwiązania dla p ∊ (7, + ∞)
|x−2| ⇒ x = 2
|x+3| ⇒ x = −3
dobra to mam tak:
na zielono: f(x) = 5
na niebiesko f(x) = 2x+1
na czerwono f(x) = −2x + 1
chyba mam źle zrobiony rysunek...
mnie wyszło, że dwa rozwiązania dla p ∊ (7, + ∞)


 dla p>5
A teraz należy się duuuuuuuuuuuża kawa
dla p>5
A teraz należy się duuuuuuuuuuuża kawa 