proch algebraiczny tomek3: Napisz wzór funkcji g, która każdej liczbie rzeczywistej m przyporządkowuje najmniejszą wartość funkcji kwadratowej f(x)=−x²+mx+m²−1 w przedziale <−1,1> Funkcja ma a<0, więc wartość największą przyjmuje w wierzchołku (p,f(p) A więc najmniejszą przyjmie gdzieś na brzegach dziedziny, albo jest to −1 albo 1 Obliczyłem f(−1)=m²−m−2 i f(1)=m²+m−2 W zależności od tego, czy m−y są dodatnie czy ujemne, f(−1)>f(1) lub f(1)>f(−1) A więc wydaje mi się, że można te 2 wzorki zwinąć w jeden : g(m)=m²+|m|−2 Co nie pokrywa się z odpowiedzią...

Mila: Trzeba rozważyć przypadki, gdzie znajduje się wierzchołek paraboli. x_w<−1, x_w∊<−1,1> x_w>1

Blee: Mila ... a nie prościej jeżeli x_w < 0 to f(1) < f(−1) (ponieważ '1' jest "dalej od wierzchołka") jeżeli x_w > 0 to f(−1) < f(1) jeżeli x_w = 0 to f(−1) = f(1)

Mila: Na to samo wyjdzie Może lepiej tak, jak TY proponujesz.

tomek3: To jak będzie wyglądał wzór tej funkcji?

Blee: ja bym zapisał tak jak Ty masz ... a jaka jest odpowiedź w książce

tomek3: xw <0 to m2+m−2<m2−m−2 czyli 2m<0 m<0 xw>0 to m2−m−2<m2+m−2 czyli −2m<0 m>0 xw=0 to m2−m−2=m2+m−2 czyli −2m=0 m=0 Tak jak pisałem, w zależności czy m będą dodatnie czy ujemne wzór funkcji będzie wyglądał inaczej, do tego już sam doszedłem Pytanie − co dalej. Ja założyłem, że te 3 wzory to to samo co m²+|m|−2 ale nie zgadza się to z odpowiedziami na końcu podr.

Blee: jeszcze raz napiszę −−−− A JAK JEST W ODPOWIEDZIACH

tomek3: @Blee Przed modułem wytrzasnęli bóg wie skąd minus : g_(m)=m²−|m|−2 Nie wspomniałem tego na samym początku, bo miałem nadzieję, że ktoś pokaże cały tok myślenia przy rozwiązywaniu

Blee: bo dla m>0 wartość mniejsza będzie dla f(−1) = m² −m − 2 a dla m<0 wartość mniejsza będzie dla f(1) = m² +m − 2 i stąd ten minus przed modułem

tomek3: pogmatwane to jakieś kurde felek

Blee: Ale teraz widzisz skąd ten minus

tomek3: no wlasnie nie co za roznica skoro modul przy opuszczeniu i tak daje przy m−ie minusa lub plusa (stosownie do dziedziny w której operujemy)

Mila: 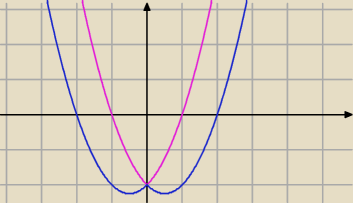♦Jest różnica bo gdzie indziej znajduje się wierzchołek. Twoja funkcja. ♦ z odpowiedzi. "Odbicie" wykresu jest z prawej na lewą.

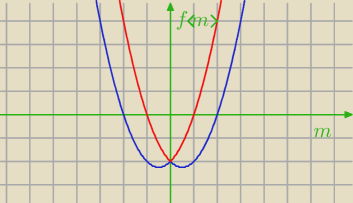
iteRacj@: to są dwie różne funkcje: g(m)=m²+|m|−2 h(m)=m²−|m|−2

iteRacj@: tak samo pomyślałam : )

tomek3: w takim razie kiedy daje − przed modulem a kiedy +?

Mila: f(x)=m²−|m|−2 Dla m≥0 mamy: |m|=m f(x)=m²−m−2 Dla m<0 mamy |m|=−m f(x)=m²+m−2

tomek3: @Mila No a jakby było f(x)=m²+|m|−2 to dla m≥0 f(x)=m²+m−2 dla m<0 f(x)=m²−m−2 No i czemu to twoje jest dobrze a to moje źle?

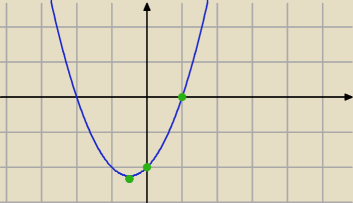
Mila: Aby naszkicować wykres funkcji g(m)=m²+|m|−2 szkicujemy wykres funkcji g(m) tylko dla m≥0 g(m)=m²+m−2

	1
mw=−		, g(0)=−2, g(1)=0
	2

rysując wykres g(m)=m²+|m|−2 pomijamy tę część wykresu ,która leży po lewej stronie OY i "odbijamy" tylko tę część z prawej to zrobię w następnym wpisie:

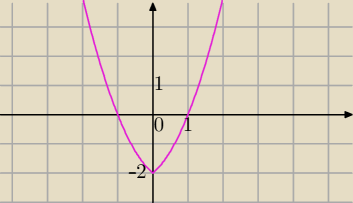
Mila: g(m)=m²+|m|−2 Czy to samo zrobić z g(m)=m²−|x|−2 ?

Mila: g(m)=m²−|m|−2 We wpisie 23:05 też źle pisałam f(x) zamiast g(m). Iteracja dobrze pisała.

Blee: ponownie wróć do mojego wpisu z 22:03 dla m<0 (czyli |m| = −m) najmniejsza wartość przyjmie funkcja w x=1 czyli: f(1) = m² +m − 2 czyli f(1) = m² − (−m) − 2 czyli f(1) = m² − |m| − 2 dla m>0 (czyli |m| = m) najmniejszą wartość przyjmie funkcja w x=−1 czyli f(−1) = m² −m − 2 czyli f(1) = m² − |m| −2

Mila: Dobranoc

tomek3: Wiem jaka będzie różnica między tymi dwoma wykresami, bo wiem w jaki sposób powstaje ta różnica mianowicie, aby powstało f(x)=m{2]+|m|−2 to wyjściową funkcją musi być h(x)=m²+m−2 na której zostaje nałożony moduł ide x>0 aby powstało g(x)= m²−|m|−2, to wyjściową funkcją musi być już m(x)=m^&#x7b;2]−m−2 na której zostanie nałożony moduł ide x>0 Analogicznie chciałbym zobaczyć jak to się dzieje bazując tylko na wzorach.

tomek3: m(x)=m²−m−2

PW: dla m>0 jest k(m)=−m dla m>0 jest k(m)=m Oznacza to, że k(m)=−|m| (patrz definicja wartości bezwzględnej). A teraz dodaj do obu stron m²−2: m²+k(m)−2=m²−|m|−2 g(m)=m²−|m|−2