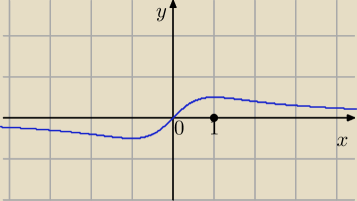
Zbadać monotoniczność i wyznaczyć ekstremum PIOPIO: f(x)=x/(x²+1) ∊R f(x)=ln(x²+1) ∊R f(x)=e⁽x²+2x) ∊R f(x)=ln(2x+1) ∊R

PW: Marne szanse. Hurtowo nie rozwiązujemy

Janek191:

	x
f(x) =
	x2 + 1

	1*(x2 + 1) − x*2 x		1 − x2
f '(x) =		=
	(x2 + 1)2		(x2 + 1)2

Dla x ∊ ( − 1, 1) jest f'(x) > 0 funkcja rośnie Dla x ∊ ℛ \ ( − 1, 1) jest f'(x) < 0 funkcja maleje oraz w x= − 1 funkcja osiąga minimum , a w x = 1 funkcja f osiąga maksimum.