trudne Oscar mat: Na boku AB równoległoboku ABCD zaznaczono punkt E, przy czym prosta CE przecina przekatną BD w punkcie K tak że |BD|=6|BK| Na boku AD zaznaczono punkt F, przy czym prosta CF przecina przekątną BD w punkcie L tak że |BD|=4|DL| Wyznacz wartość ilorazu (|AE|*|AF|) / (|EB|*|FD|) W żaden sposób nie mogę sobie poradzić z tym zadaniem, pomoże ktoś?

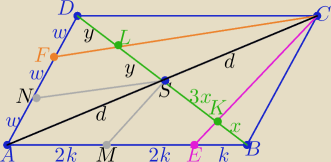
Eta: 1/ rysunek i wprowadź oznaczenia zgodne z treścią 2/ przekątne równoległoboku przecinają się w punkcie S i dzielą na połowy 3/ dorysuj odcinki SM i SN równoległe odpowiednio do CE i CF 4/ poproś 4 razy Talesa ( i zaznacz następne dane na rysunku i wszystko będzie jasne Odp: wartość tego ilorazu = 8

Eta: Na rysunku pomyłkowo wpisałam 3x a ma być 2x bo |BD|=6x to |BS|=3x więc |KS|=2x