Algerba Satan: Jak narysować wykres krzywej 2x² − y² = 1? Wyliczam:

	2 0 0 −1	x y
(x y)			= 1

Rozwiązanie jest postaci λ₁(x')² + λ₂(y')² = 1 Wyliczam wartości własne: (2 − λ)(−1 − λ) = 0 Czyli λ₁ = −1, λ₂ = 2

	0 y		x 0
Wektory własne dla kolejnych wartości własnych to:		,

	0 1		1 0
Czyli nowy układ jest starym układem, bo wersory mają współrzędne		i		.

Tylko co teraz? Nie bardzo nawet wiem, czy dobrze to dotąd robię.

Satan:

	x
Dobra, już wiem. Przekształcam do postaci (		)2 + y2 = 1
	1   √2

	1		1
Stąd		i −		to asymptoty krzywej.
	√2		√2

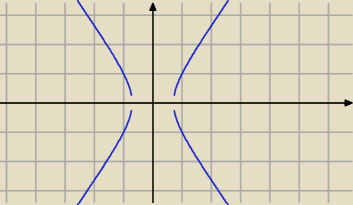Mila: 2x² − y² = 1 Hiperbola

ABC: tak w kwestii formalnej: to co on napisał w pierwszej linijce o 22:06 to elipsa jest

Mila: https://pl.wikipedia.org/wiki/Hiperbola_(matematyka)

Satan: Tak, ABC słusznie wyłapał, tam przy y² powinien być znak minusa