geometria kasia : Proszee o pomoc! W trójkącie prostokątnym przyprostokątne mają długość 12 cm i 5 cm. Przez wierzchołek kąta prostego poprowadzono prostą, która podzieliła ten trójkąt na dwa trójkąty o różnych obwodach. Oblicz stosunek długości promieni okręgów wpisanych w powstałe okręgi.

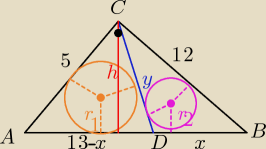Eta: z tw. Pitagorasa wyznaczamy IABI= √5²+12²= √169= 13 Ob(ADC) = Ob(DBC) , ponieważ y −− jest wspólnym bokiem tych trójkątów to 5+13−x = x+12 => 2x = 6 => x=3 zatem : IADI= 10 i IDBI= 3

	P
ro .wp=		, p−− połowa obwodu Δ−ta
	p

	P(ΔADC)
to r1=
	p1

	P(ΔBDC)
r2=
	p2

ponieważ obwody tych trójkątów są równe , to ; p₁=p₂ i wysokości tych trójkątów są też równe h to:

	r1		PΔADC		12*10*h		10
		=		=		=
	r2		PΔBDC		12*3*h		3

	r1		10
Odp:		=
	r2		3

Zielona Gałązka: Eta, jestem pełna podziwu dla Ciebie Piękny rysunek i tok wytłumaczenia. Tylko kruca bomba proszę oświeć mnie, dlaczego te obwody są równe? Czy jest takie twierdzenie w matmie? Bo ja nie słyszałam. Pozdrówka serdeczne.

Eta: Hehe Są tu lepsi od rysowania A co do równych obwodów .... z treści zadania .... przeczytaj Też pozdrawiam

Eta: Oczywiście ,że Kasia, zamiast "równych" , napisała " różnych " ! ale domyśliłam się ,że powinno być równych obwodach, bo inaczej to nie da się tego zad. rozwiązać, ......achch... ta nasza młodzież

kasia : o kurde no faktycznie dzieki baaardzoooo