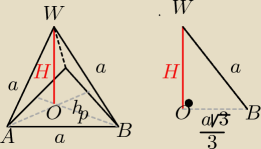Bryły fryk: Czworościan foremny ma objętość równą 2 pierwiastki z dwóch. Jaką długość ma krawędź tego czworościanu?

fryk: Pomożecie?

Godzio: https://matematykaszkolna.pl/strona/989.html

Eta: czworościan foremny , to ostrosłup ,którego wszystkie ściany i podstawa są trójkątami równobocznymi

	a√3
hp=
	2

	a√3
IOBI= 23hp=
	3

z ΔOBW z tw. Pitagorasa H²= a² −(a√3/3)² = a² −^a2₃= ²₃*a²

	a√6
to H=
	3

podstaw dane do wzoru na V

	a2√3
V= 13*		*H = 2√2
	4

i wyznacz "a" odp: a= ³√24 [j ]

Eta:

fryk: Dziękuję Ci bardzo Eto.

Eta: Ech ..... lenuiszek z Ciebie

fryk: Eto, mam jednak pytanie. Próbuję już n−ty raz i nadal nie wychodzi mi, jak doszłaś do H ? Chodzi mi tylko o odliczenia , bo mi w pewnym momencie wychodzi coś takiego: H²= a² − a²/3 /*3 3H²=a² − a²

Eta: a ile jest?... 1−¹₃ .... = ²₃ tak? to a²− ¹₃a² = ²₃a²

	√2		√6
więc H2= 23a2 to H= a		= a*
	√3		3

fryk: Teraz wiem, gdzie robiłam błąd. Dziękuję jeszcze raz

Eta: Zobacz co Ty napisałeśs pokazuję błąd: H²= a² −a²/3 \*3 3H²= 3a² −a² = 2a²

	2a2
to H2=
	3

	√2		√6
więc H= a*		= a*		....... teraz czyli ok
	√3		3

Martusia:

ania: Hej a możesz wytłumaczyć krok po kroku jak obliczyłeś V bo nie wychodzi mi V =

Sherlock: Czworościan foremny jest ostrosłupem, a objętość ostrosłupa to jedna trzecia iloczynu pola podstawy przez wysokość. Podstawą naszej bryły jest trójkąt równoboczny o krawędzi a. Pole takiego trójkąta to

	√3
P = a2		− w zasadzie wzór ten trzeba pamiętać.
	4

	1
Można go też wyprowadzić z podstawowego wzoru na pole trójkąta P =		a h . Ponieważ
	2

wszystkie boki trójkąta mają tę samą długość, jego wysokość h możemy obliczyć z tw. Pitagorasa:

	1
a2 = (		a)2 + h2 (dlaczego tak? jeśli nie rozumiesz, narysuj sobie trójkąt równoboczny
	2

i w nim wysokość, wtedy wzór stanie się jasny)

	1		1
h2 = a2 −		a2 (do kwadratu podnosimy nie tylko a, ale także liczbę		)
	4		2

Całość minus ćwiartka to trzy ćwiartki, zatem:

	3		√3
h2 =		a2 , czyli h =		a
	4		2

Wyprowadzony wzór na wysokość trójkąta równobocznego wstawiamy do wzoru na pole:

	1		1		√3		√3
P =		a h =		a *		a = a2		(otrzymaliśmy wzór, który w
	2		2		2		4

zasadzie trzeba i tak pamiętać...)

	√6
Wyżej Eta wyprowadziła wzór na wysokość bryły: H = a
	3

	1
Wstawiamy odpowiednie wyrażenia do ogólnego wzoru na objętość ostrosłupa V =		P H
	3

	1		√3		√6
V =		* a2		* a
	3		4		3

Wzór ten możemy uprościć, wykonując odpowiednie mnożenia:

	√3 √6
V =		* a3
	3 * 4 * 3

Rozkładamy pierwiastek z sześciu na czynniki:

	√3 √3 √2
V =		* a3
	3 * 4 * 3

Dwa mnożone przez siebie pierwiastki z 3 skrócą się z trójką w mianowniku:

	√2
V =		* a3
	4 * 3

	√2
V =		* a3
	12

(ten wzór znajduje się w zestawieniu najważniejszych wzorów dla gimnazjum, więc być może trzeba go pamiętać... zawsze jednak trzeba go umieć sobie wyprowadzić) W zadaniu wiadomo, że V = 2 √2 i mamy z tego wyznaczyć a. Pokażę to obliczenie tak łopatologicznie. Zaczynamy od wstawienia za V znanej wartości:

	√2
2 √2 =		* a3
	12

Zamieniamy strony miejscami, żeby mieć a po lewej:

√2
	* a3 = 2 √2
12

Obie strony dzielimy przez √2 :

1
	* a3 = 2
12

Obie strony mnożymy przez 12: a³ = 24 a = ³√24 Możemy jeszcze wyciągnąć, ile się da, przed znak pierwiastka... W tym celu rozkładamy wyrażenie podpierwiastkowe na czynniki: a = ³√2 * 2 * 2 * 3 Wyciągamy czynnik, który powtarza się trzy razy (bo mamy pierwiastek stopnia trzeciego): a = 2 √3 Gotowe!

Sherlock: a = 2 ³√3 oczywiście ma być

Mila: V=2√2

	a3√2
V=		⇔
	12

a3√2
	=2√2
12

a³=24 a=³√24=³√8*3 a=2³√3 =====