Trudniejsze zadanko z parametrem i funkcji kwadratowej tomek3: Trudniejsze zadanko z parametrem i funkcji kwadratowej Wyznacz wszystkie wartości parametru m, dla których rownanie 4x²−4m|x|+6m−9=0 ma takie 2 rozwiązania, że x₁+x₂=0 Na samym początku zadałem sobie pytanie, co w ogóle zmienia mi ten moduł. Bo skoro −b/a i tak ma być równe zero, to i tak m będzie równe zero dla każdego xa, niezależnie czy jest to x>0 (x) czy x<0 (−x) Tak samo z deltą od m, bez różnicy mi to czy jest to x czy −x, bo i tak podnoszę b do kwadratu (b²−4ac) No ale moje rozumowanie jest błędne, bo odpowiedź jest całkowicie inna niż myślałem.

tomek3: Tzn żeby mnie ktoś źle nie zrozumiał, ja wiem, że w takich zadankach w zasadzie operuje się tylko na m−ach i właśnie chodziło mi o to, że gdyby zamiast modułu był np −x to wtedy − przechodzi mi na m−y i np. nie mam wtedy −4m tylko 4m, ale to i tak nic nie zmienia.

ABC: zostaw ty chłopie te delty i zrób sztuczkę techniczną korzystając z równości (2|x|−m)²−m²=4x²−4m|x| dostajesz po przekształceniach równanie: (2|x|−m)²=(m−3)²

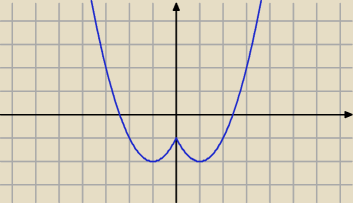
Mila: Dlaczego zakładasz m=0? (parabola, w której osią symetrii jest OY) Tu masz wykres f(x)=x²−2|x|−1 masz spełniony warunek x₁+x₂=0 Na natępnym rysunku podam przykład, gdy nie jest spełniony.

Mila: 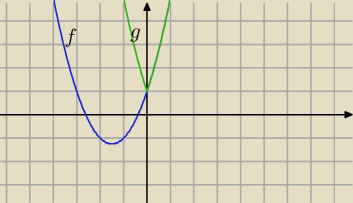f(x)=x²+3x+1 g(x)=x²+3|x|+1

Tadeusz: Ty zrób inną "sztuczkę" ... wymyslił ją Vieta

ABC: Tadeusz do mnie to mówisz? wzory Vieta nie obowiązują gdy w równaniu kawdratowym x jest pod znakiem wartości bezwzględnej

Tadeusz: ... tak tak ... postukaj sie w głowę i pomyśl czemu budzę tego Viete'a

tomek3: @Mila no bo ze wzorow Viete'a mam właśnie, że −b/a=0 b=−4m (x>0) b=4m (x<0) a=4 czyli niezależnie od tego, czy moduł opuszczony został zostawiając x z minusem czy bez, to i tak równanie to będzie miało 2 pierwiastki spełniające równanie x1+x2=0 dla m=0

tomek3: −4m/0=0 −−> m=0 4m/0=0 −−−> m=0 czemu to jest źle?

tomek3: −4m/4=0 −−> m=0 4m/4=0 −−−> m=0 przepraszam pomylka z mianownikiem

Tadeusz: ... tak to nie

ABC: Tomek masz równanie: x²−3|x|+2=0 ile według ciebie ono ma pierwiastków i ile wynosi ich suma?

Tadeusz: ... Mila już wam to wyjasniła. Równanie 4x²−4mx+6m−9=0 musi mieć − jeden pierwiastek dodatni lub − dwa pierwiastkiróżnych znaków

tomek3: @ABC

	⎧	x2−3x+2 gdy x>0
f(x)=	⎩	x2+3x+2 gdy x<0

ta pierwsza funkcja : delta : 9−4*2=1 x1=(3−1)/2=1 >0 x2= (3+1)/2=2 >0 (użyłbym wzórów vieta, ale chcialem sprawdzic, czy pierwiastki ktore wyjda beda zgadzac sie z dziedzina) x1+x2=3 ta druga funkcja : delta : 9−4²=1 x1=(−3−1)/2=−2 x2=(−3+1)/2=−1 x1+x2=−3 suma ich wszystkich to 3+(−3)=0

tomek3: @Tadeusz ale ja nadal nie wiem jakim sposobem to zadanie powinno zostać zrobione

ABC: jeśli chodzi o wyjściowe równanie to może mieć ono dwa, trzy lub cztery pierwiastki przy czym ma pierwiastki x=−3/2 i x=3/2 niezależnie od wartości m dla m=3/2 ma trzeci pierwiastek x=0 dla m>3/2 ma trzeci i czwarty pierwiastek x=√m−3/2, x=−√m−3/2

Tadeusz: zacznij od tego, że wykres funkcji f(x)=4x²−4m|x|+6m−9=0 dla x≥0 jest identyczny jak wykres f(x)=4x²−4mx+6m−9=0 a dla x<0 ... jest jaki ?

ABC: dla m=3.75 wynika stąd istnienie dwóch pierwiastków podwójnych

tomek3: @Tadeusz tak jak wczesniej pisalem − dla x<0 wzor jest taki : 4x²+4mx+6m−9 i chodzi mi o to, że niezależnie od tego czy x<0 czy x>0 to i tak −b/a będzie równe zero tylko i wyłącznie dla m=0 z deltą tak samo, niezależnie, czy zamiast 4mx będzie −4mx to delta m > 0 wtedy i tylko wtedy, gdy (m−3)²>0 czyli m należy do (−niesk, 3) suma (3, niesk)

tomek3: m należy do (−niesk, 3/2) suma {3}

ABC: no i tak jest jak napisał o 19.22

tomek3: zadanie 2.59 https://imgur.com/a/hKptGB2 a ta odpowiedź to w ogole nic mi nie wyjasnia

ABC: z tego co napisałem o 17.51 wynika alternatywa |x|=3/2 v |x|=m−3/2 więc dla m=3 są tylko 2 pierwiastki bo warunki się pokrywają

tomek3: @ABC No spoko, ale to jest repetytorium do matury rozszerzonej i nie zależy mi na konkretnym wyniku, bo ten mam precyzyjnie podany na końcu podr., tylko o sposób rozwiązania. O ile macie chęci i umiejętności, to bardzo bym prosił, żeby ktoś mi to wytłumaczył.

tomek3: oczywiscie nie mialo to zabrzmiec jakbym kwestionowal wasze umiejetnosci

tomek3: bo moje pewnie nie umywaja sie w 1/1000 do waszych

ABC: Tomek przykro mi że nie rozumiesz mojego sposobu bo on jest najkrótszy

Tadeusz: tomek3 skup się jak rysujemy wykres funkcji f(x)=4x²−4m|x|+6m−9=0 ?

Tadeusz: pisałe Ci o tym o 19:01

tomek3: robimy symetrię względem osi OY wyjściowego wykresu paraboli dla każdego x<0

Tadeusz: jasne

Tadeusz: to teraz przeczytaj co napisalem o 18:49

tomek3: "Równanie 4x2−4mx+6m−9=0 musi mieć − jeden pierwiastek dodatni lub − dwa pierwiastkiróżnych znaków" z tym drugim sie zgodze, jako iz x1+x2=0 czyli x1=−x2 ale jezeli mamy tylko jeden pierwiastek, to musialoby to byc chyba 0? bo przeciez w kazdym innym przypadku nie spelnialoby warunku zadania

tomek3: poza tym w poleceniu jest napisane, "ma takie DWA RÓŻNE rozwiązania"

Tadeusz: Czytaj uważniej : mówię o równaniu 4x²−4mx+6m−9=0

PW: YES, YES, YES.

PW: Tadeusz, pamiętam jak mnie kiedyś chciałeś zniszczyć psychicznie z powodu mylnego zrozumienia zadania. Przepraszam stokrotnie i jeszcze raz. Uważasz od tego czasu, ze zawsze bredzę? Nie masz jakichś kłopotów z własną psychiką? Proszę. odpierdol się ode mnie raz na zawsze. Ani w tym, ani w innym zadaniu nie podejmuję z tobą polemiki, nie zauważyłeś?

xxx: ale meksyk xD

ABC: jak w naszym Sejmie dobra żeby było trochę merytorycznie dokończę te przekształcenia z 17.51 może Tomek zrozumie: (2|x|−m)²=(m−3)² 2|x|−m=m−3 v 2|x|−m=3−m 2|x|=2m−3 v 2|x|=3 |x|=m−3/2 v |x|=3/2 i z tej postaci widać to o czym wcześniej pisałem, że zawsze są dwa rozwiązania x=−3/2 , x=3/2 itd.

Eta: Hej Panowie pedagodzy ! ! A może pogodzę Was

xxx: #team_PW

tomek3: nie zgodzić* 2038 @ABC Ale skąd w ogóle wziąłeś tę równość? Skąd ona wynika? Bo ja nie mam pojęcia. Napisałeś tylko "zobacz tę sztuczkę techniczną". No dobra, ale skąd ona w ogóle się wzięła, z jakich wniosków wypłynęła? Bo ja na pierwszy rzut oka tego nie rozumiem. Poza tym, rozwiązanie ma być w formie nierówności.

ABC: tomek a wiesz że równania kwadratowe można oprócz delty rozwiązać metodą dopełniania do kwadratu? przykład x²+6x−7=0 x²+6x+9−16=0 x²+6x+9=16 (x+3)²=4² x+3=4 v x+3=−4 x=1 v x=−7 coś takiego zastosowałem tylko w bardziej skomplikowanej otoczce

purple: @tomek3, wynika z pomysłu, doświadczenia, trochę innego spojrzenia. To nie jest tak, że od razu będziesz wpadał na takie pomysły. Dopiero z czasem, po przerobieniu iluś zadań zaczniesz próbować czegoś innego niż takich tradycyjnych, schematycznych metod pokazywanych w podręcznikach czy na lekcjach.

Mila: (1) 4x²−4m*|x|+6m−9=0 x²=|x|², podstawienie: |x|=t, t>0 (2) 4t²−4m*t+6m−9=0 Δ=16m²−16(6m−9)= 16*(m−3)² a) Jeżeli f(t)=4t²−4m*t+6m−9 ma ma jedno miejsce zerowe i dodatnie to równanie (1) ma dwa rozwiązania , które są liczbami przeciwnymi. (przykład: t=2 wtedy |x|=2 ⇔x₁=2 lub x₂=−2 i mamy: x₁+x₂=0 ) Zatem :

	−b
Δ=0 i t=		>0
	2a

	4m		m		3		3		3		3
m=3 i t=		=		=		czyli |x|=		, stąd X1=		lub x2=−
	2*4		2		2		2		2		2

lub b) Równanie (1) ma dwa rozwiązania , które są liczbami przeciwnymi, jeżeli równanie (2) ma rozwiązania różnych znaków (np: t₁=−3 lub t₂=4 wtedy t₁ =−3 "odrzucamy",|x|=4 to x₁=4 lub x₂=−4 i pasuje) Δ>0 i t₁*t₂<0⇔

	c		6m−9		3
m∊R\{3} i		=		<0⇔m<
	a		4		2

odpowiedź:

	3
x∊{−∞,		)∪{3}
	2

==============

tomek3: @PW A odrobiny poczucia humoru nie masz. @ABC @Mila Podobne rzeczy robiliśmy przy "zwijaniu" okręgów, ale jednak wolałbym coś prostszego do zapamiętania, bardziej schematycznego z większą szansą, że nie zapomnę do matury. @Mila pomożesz?

tomek3: @Mila zacząłem pisać przed twoim postem

Mila: Analizuj to, co wpisałam i mam nadzieję, że już będzie jasne

tomek3: no juz rozumiem, dzieki @Mila trudne zadanko

Mila: