Znajdź ekstrema oraz przedziały monotoniczności funkcji
ela: Znajdź ekstrema oraz przedziały monotoniczności funkcji
f(x)= xex
Rozwiąż zadanie, a następnie wśród odpowiedzi znajdź te, które są prawdziwe.
Wybierz jedną lub więcej:
Funkcja posiada maksimum dla .x=1
Funkcja posiada minimum dla .x=0
Funkcja maleje w przedziale (.0,1)
Funkcja maleje w przedziale .(−∞,1)
Funkcja ma dziedzinę równą .r
10 gru 20:43
Janek191:
Funkcja ma dziedzinę ℛ, a nie r.
10 gru 20:47
ela: niedopatrzenie
10 gru 20:48
Janek191:
Oblicz pochodną f.
10 gru 20:51
ela: 1−xex
10 gru 20:55
10 gru 20:56
ela: a nie powinno być zamiast x , 1−x?
10 gru 20:57
Janek191:
| | 1 − x | |
f '(x) = |
| , ex > 0 |
| | ex | |
Określ znak pochodnej .
10 gru 20:58
ela: x=1
10 gru 20:58
Janek191:
Tak, dla x = 1 f"(x) = 0
Dla x < 1 jest f '(x) > 0
Dla x > 1 jest f '(x) < 0
zatem funkcja ma ekstremum w x = 1 ( jakie ?)
Gdzie rośnie , a gdzie maleje f ?
10 gru 21:01
ela: x=1 maksymalne
rośnie od (−∞,1) maleje od (1,∞)
10 gru 21:02
ela: na odwrót chyba
10 gru 21:03
Janek191:
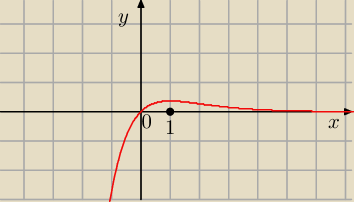
W x = 1 f osiąga maksimum
Rośnie w ( −
∞, 1), maleje w ( 1, +
∞)
10 gru 21:05
ela: okej czyli będzie odpowiedź;
Funkcja posiada maksimum dla .x=1
Funkcja ma dziedzinę równą .R
10 gru 21:09
Janek191:
10 gru 21:17
ela: Dziękuję
10 gru 21:26