ta tomek3: wyznacz rownanie prostej do ktorej nalezy punkt P(−6,15) i takiej ze odleglosc punktu Q(4,−5) od tej prostej wynosi 10 wyszlo mi jedno rownanie y=−3/4x+21/2 i jest ono poprawnem aczkolwiek zniknelo mi gdzies x−6=0

Satan: Oznaczmy szukaną prostą w postaci ogólnej jako k: Ax + By + C = 0 Z warunków zadania wiemy, że: P ∊ k i odległość Q od k jest równa 10 Z pierwszego warunku otrzymujemy: A(−6) + B(15) + C = 0 ⇒ C = 6A − 15B

	|Ax0 + By0 + C|
Skorzystajmy ze wzoru na odległość punktu od prostej:		= d
	√A2 + B2

Z drugiego warunku mamy:

|A(4) + B(−5) + C|
	= 10
√A2 + B2

Po podstawieniu C = 6A − 15B:

|4A − B5 + 6A − 15B|
	= 10
√A2 + B2

|10A − 20B| = 10√A² + B² Teraz obie strony podnosimy do kwadratu − możemy to zrobić, bo obie strony są dodatnie: (10A − 20B)² = 10(A² + B²) 100A² − 400AB + 400B² = 100A² + 100B² 300B² − 400AB = 0 100B(3B − 4A) = 0 Czyli B = 0 lub 3B − 4A = 0 Rozpatrzmy przypadek, gdy B = 0: C = 6A − 15B Więc po podstawieniu mamy: C = 6A Korzystając z niejednoznaczności postaci ogólnej wybierzmy sobie A = 1, wtedy: C = 6 Otrzymujemy więc prostą postaci: x + 6 = 0 (jest to inna prosta niż ta podana przez Ciebie, ale zauważ, że punkt P nie należy do prostej o równaniu x − 6 = 0) Zajmijmy się przypadkiem 3B − 4A = 0. Stąd otrzymujemy 3B = 4A. Znów skorzystajmy z niejednoznaczności postaci ogólnej przyjmując A = 1: 3B = 4

	4
B =
	3

Wróćmy do C = 6A − 15B

	4
C = 6*1 − 15*
	3

C = 6 − 20 C = −14 Dostajemy prostą o równaniu:

	4
x +		y − 14 = 0
	3

3x + 4y − 42 = 0 Szukane proste są opisane równaniami: x + 6 = 0 3x + 4y − 42 = 0

Tojatpy: Co to jest niejednoznacznosc postaci ogolnej? Dlaczego podstawiles sobie za A jedynke mimo ze nie bylo wyliczone?

Satan: Równanie ogólnej prostej jest niejednoznaczne. Znaczy to tyle, że jedną prostą można zapisać na wiele sposobów. Np: x + y + 1 = 0 10x + 10y + 10 = 0

3		3		3
	x +		y +		= 0
2		2		2

Wszystko to ta sama prosta. I zauważ, że KAŻDY współczynnik możemy przekształcić do dowolnej liczby. Dajmy na to: 3x + 5y − 17 = 0 Chcemy mieć A = 2:

	2
3x + 5y − 17 = 0 / *
	3

	10		34
2x +		y −		= 0
	3		3

I jak widać jest to ta sama prosta, co 3x + 5y − 17 = 0. Wystarczy pomnożyć równanie przez

	3
		.
	2

Dlatego ta postać jest lepsza, niż y = ax + b, a przynajmniej w tym przypadku Przyjąłem A = 1, bo... Tak jest najłatwiej. Równie dobrze możesz przyjąć inne liczby za A lub B.

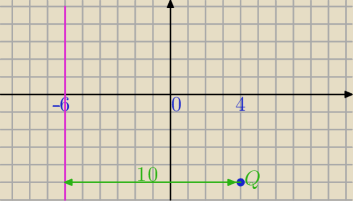
Mila: Wykorzystując równanie kierunkowe prostej: y=ax+b nie otrzymasz pionowych prostych ( prostopadłych do OX) a=tgα, a tg 90 ^o nie istnieje. Bezpieczniej jest wykorzystywać równanie postaci ogólnej. Możesz też skorzystać z rysunku (ale to nie zawsze się da). Dla Toja.. piszę rozwiązanie, trochę inne rachunki niż Satana k: Ax+By+C=0− równanie szukanej prostej,P∊k Q=(4,−5), P=(−6,15) A*(−6)+B*15+C=0 C=6A−15B Mamy równanie: Ax+By+6A−15B=0

	|A*4−5B+6A−15B|
d(Q,k)=10=		⇔
	√A2+B2

|10A−20B|=10*√A²+B² /:10 |A−2B|=√A²+B² /² A²−4AB+4B²=A²+B² −4AB+3B²=0⇔ B*(−4A+3B)=0 B=0 lub 3B=4A 1) B=0 ⇔Ax+0y+6A−15*0=0 Ax+6A=0 /:A k₁: x+6=0 lub

	3
2) A=		B
	4

3		3
	Bx+By+6*		B−15B=0 /*4
4		4

3Bx+4By+18B−60B=0 B*(3x+4y−42)=0 , (3x+4y−42)=0 , k₂: 3x+4y−42=0

PW: Przypomnę jak to się robiło za pomocą cyrkla i linijki. Analiza zadania Szukamy punktu R, takiego że a) PR⊥RQ i b) |RQ| = 10. Punkt ten pozwoli wyznaczyć prostą PR, a Q leży w odległości 10 od tej prostej. Jak wiadomo warunek a) jest spełniony wtedy i tylko wtedy, gdy R należy do okręgu o średnicy PQ. Warunek b) jest spełniony wtedy i tylko wtedy, gdy R należy do okręgu o środku Q i promieniu 10. Konstrukcja Tu rysowało się dwa okręgi (by wyznaczyć środek odcinka PQ), a następnie okręgi opisane wyżej i po wyznaczeniu ich punktów wspólnych R₁ i R₂ rysowało się proste PR₁ oraz PR₂ KONIEC My musimy to niestety wyliczyć, w tym zadaniu rachunki są przy każdym podejściu dość mozolne.

	−6+4		15−5
a) Środek okręgu to punkt S = (		,		) = (−1, 5). Promień okręgu to r, gdzie
	2		2

r² = |PS|² = (−1+6)²+(5−15)² = 125. Równanie okręgu: (1) (x+1)² + (y−5)² = 125. b) Równanie okręgu o środku Q: (2) (x−4)² + (y+5)² = 10². Szukany punkt R należy do obydwu okręgów, jego współrzędne spełniają układ równań (1) i (2): (1') x²+2x+y²−10y = 99 (2') x²−8x+y²+10y = 59, z którego po odjęciu stronami 10x−20y = 40 (3) x=2y+4 Podstawienie (3) do (1') daje (2y+4)²+2(2y+4)+y²−10y = 99 5y²+10y−75 = 0 y²+2y−15 = 0 (y+5)(y−3)=0 y₁=−5, y₂=3 i po podstawieniu do (3) x₁=−6, x₂ = 10 R₁ = (−6, −5), R₂ = (10, 3) Szukana prosta przechodzi przez R₁ i P lub R₂ i P. Dla R₁ i P mamy jednakowe pierwsze współrzędne, a więc prosta jest pionowa, ma równanie x=−6. Dla R₂ i P prosta ma równanie y=ax+b, przy czym

	⎧	3=a•10+b
	⎩	15=a•(−6)+b	,

	3		42
skąd a=−		i b=−
	4		4

	−3		42
y=		x+		− to samo równanie co u Mili równanie prostej k2.
	4		4

Mila: Witam PW, zanim podałam rozwiązanie, to właśnie była na kartce konstrukcja. Pozdrawiam