geo analit
tomek3: W trójkącie prostokątnym ABC przy wierzchołku B 90. dwa wierzchołki maja współrzędne A(4; −5)
C(−8; 5) wyznacz współrzędne wierzchołka B wiedząc że pole wynosi 61
9 gru 21:40
the foxi:
zauważ, że |AC|=2
√61
więc wysokość opuszczona z wierzchołka B na AC musi mieć długość
√61
narysuj to np. na kartce, na pewno zauważysz, co dalej

9 gru 22:21
Mila:
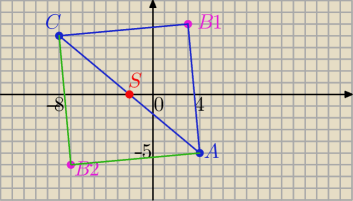
A(4; −5) C(−8; 5) , B=(p,q)
BC
→=[−8−p,5−q], BA
→=[4−p,−5−q]
1) |AC|=
√122+102=
√244=2
√61
√61*h=61
h=
√61
2) Prosta AC:
−5=4a+b i 5=−8a+b
6y=−5x−10=0
5x+6y+10=0
3) B(p,q) leży w odległości h=
√61 od prostej AC
| | |5*p+6*q+10| | |
d= |
| =√61 |
| | √52+62 | |
|5p+6q+10|=61⇔
5p+6q+10=61 lub 5p+6q+10=−61
5p+6q=51 lub 5p+6q=−71
4) BC
→⊥BA
→⇔[−8−p,5−q] o [4−p,−5−q]=0 iloczyn skalarny równy 0.
(−8−p)*(4−p)+(5−q)*(−5−q)=0⇔p
2+4p+q
2=57
a)5p+6q=51 i p
2+4p+q
2=57⇔
p=3, q=6
B
1=(3,6)
lub
5p+6q=−71 i p
2+4p+q
2=57⇔
p=−7, q=−6
B
2=(−7,−6)
==========
9 gru 23:48
tomek3: dz
10 gru 00:22
Eta:
|AC|=2√61 i P=61 to h=|BS|=√61 gdzie S środek AC : S(−2,0) i B(x.y)
Z warunku prostopadłości wektorów SB ⊥ SA ,
→ →
SA=[6,−5] i SB=[x+2, y] to [x+2,y]=[5,6] lub [−5,−6]
zatem x+2=5 i y=6 lub x+2=−5 i y= −6
x=3 i y=6 lub x= −7 i y=−6
B(3,6) lub B(−7,−6)
10 gru 00:32
Tojatpy: Skad wiemy ze wysokosc hb przecina nok przeciwny na dwie polowy?
10 gru 07:01
Mila:
Właśnie zamknęłam wczoraj komputer i stwierdziłam, że w tym zadaniu moja metoda
jest "nieekonomiczna." Strzeliłam z armaty do wróbla.
Eta to zauważyła. Dzięki za rozwiązanie.

Moje rozwiązanie :
|AC|=2
√61− dł. przeciwprostokątnej
√61− dł. wysokości poprowadzonej do przeciwprostokątnej jest równa połowie
przeciwprostokątnej
⇔ΔABC − trójkąt prostokątny równoramienny
Spodek wysokości leży w punkcie S=(−2,0)
|SA|=|SB|
SA
→=[6,−5]
SA⊥SB⇔
SB
→=[5,6] wtedy: S(−2,0)→T
[5,6]→B
1=(3,6)
lub
SB
→=[−5,−6]
Wtedy: S(−2,0)→T
[−5,−6]→B
2=(−7,−6)
============================
10 gru 15:30

 A(4; −5) C(−8; 5) , B=(p,q)
BC→=[−8−p,5−q], BA→=[4−p,−5−q]
1) |AC|=√122+102=√244=2√61
A(4; −5) C(−8; 5) , B=(p,q)
BC→=[−8−p,5−q], BA→=[4−p,−5−q]
1) |AC|=√122+102=√244=2√61
 Moje rozwiązanie :
|AC|=2√61− dł. przeciwprostokątnej
√61− dł. wysokości poprowadzonej do przeciwprostokątnej jest równa połowie
przeciwprostokątnej
⇔ΔABC − trójkąt prostokątny równoramienny
Spodek wysokości leży w punkcie S=(−2,0)
|SA|=|SB|
SA→=[6,−5]
SA⊥SB⇔
SB→=[5,6] wtedy: S(−2,0)→T[5,6]→B1=(3,6)
lub
SB→=[−5,−6]
Wtedy: S(−2,0)→T[−5,−6]→B2=(−7,−6)
============================
Moje rozwiązanie :
|AC|=2√61− dł. przeciwprostokątnej
√61− dł. wysokości poprowadzonej do przeciwprostokątnej jest równa połowie
przeciwprostokątnej
⇔ΔABC − trójkąt prostokątny równoramienny
Spodek wysokości leży w punkcie S=(−2,0)
|SA|=|SB|
SA→=[6,−5]
SA⊥SB⇔
SB→=[5,6] wtedy: S(−2,0)→T[5,6]→B1=(3,6)
lub
SB→=[−5,−6]
Wtedy: S(−2,0)→T[−5,−6]→B2=(−7,−6)
============================