Stereometria matlamp: Na półsferze o promieniu R leżą dwa styczne do siebie okręgi o promieniu r.Wyznacz największą odległość między dwoma punktami należącymi do tych okręgów.

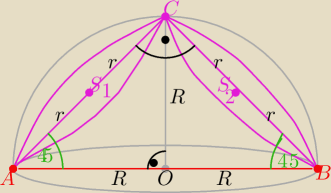
Eta: d_max=|AB|=2R i 2r=R√2 ⇒ R=√2r to d_max=2R=2√2r ============

matlamp: Łuk AC nie powinnien miec dlugosc 2r zamiast odcinka AC, skoro okregi leza na polsferze?

Eta: Średnica |AC|=2r

Eta: Weź pomarańczę przekrój na pół i połóż na stole Teraz odetnij z obydwu stron dwie części styczne w punkcie C i w punktach najdalej wysuniętych A i B na kole wielkim półsfery W przekroju otrzymasz trójkąt prostokątny i równoramienny ................ jak pisałam wyżej

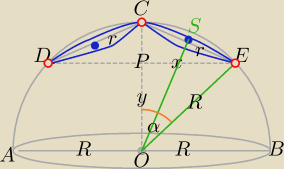
Mila: |EP|=x, 0<x≤R 1) W ΔCOE: (2r)²=R²+R²−2R²cosα

	R2−2r2
cosα=
	R2

2) w ΔOPE:

	y
cosα=
	R

R2−2r2		y
	=
R2		R

	R2−2r2
y=
	R

x²+y²=R²

	2r√R2−r2
x=
	R

3)

	4r√R2−r2
|DE|=
	R

======================= 4) dla przypadku 2r=R√2 mamy:

	R√2
r=
	2

|DE|=2R

Eta: W treści przeczytałam : "wyznacz największą odległość