maturalne zadanie MATURAAAAAAAA: Z punktu A = (3,0) poprowadzono styczne do okręgu x² + y² − 2x = 0. Styczne te przecinają prostą o równaniu y=√3x+√3 w punktach B i C. Wyznacz pole trójkąta ABC.

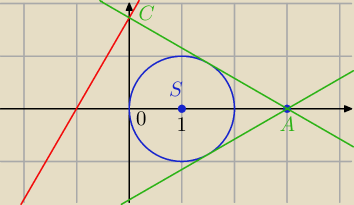
Janek191: x² + y² −2 x = 0 (x − 1)² − 1 + ( y − 0)² = 0 (x −1)² + ( y − 0)² = 1 S = ( 1, 0) r = 1 y = a x + b ⇒⇒ a x − y + b = 0 A = ( 3, 0) więc 3 a − 0 + b = 0 ⇒ b = −3a Mamy zatem a x − y −3 a = 0 Odległość prostej od S = ( 1, 0) = r = 1, więc

I a*1 − 1*0 − 3 a I
	= 1
√a2 + 1

I − 2 a I = √a² + 1 2 I aI = √a² + 1 4 a² = a² + 1 3 a² = 1

	1
a2 =
	3

	1		1
a = −		lub a =
	√3		√3

b = √3 lub b = − √3 zatem styczne mają równania:

	√3		√3
y = −		x + √3 lub y =		− √3
	3		3

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− Dokończ