Podstawą ostrosłupa ABCS jest trójkąt prostokątny ABC o kącie prostym przy... PGinf: Podstawą ostrosłupa ABCS jest trójkąt prostokątny ABC o kącie prostym przy wierzchołku C. Każda krawędź boczna ostrosłupa ma długość 7. Ściana ASC jest nachylona do płaszczyzny podstawy pod kątem o mierze 45°, a ściana BSC pod kątem o mierze 60°. Oblicz pole przekroju ostrosłupa ABCS płaszczyzną zawierająca krawędź CS i wysokość ostrosłupa. Odpowiedź : 7√3

PGinf: Zadanie z Kiełbasy, jedno z tych chyba trudniejszych, ale jak by ktoś potrafił zrobić to super

Mila:

	1
PΔSOC=		H*|OC|
	2

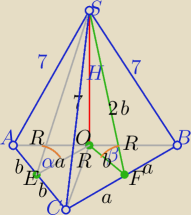
1) Wszystkie krawędzie boczne są równe⇔spodek wysokości H leży w środku okręgu opisanego na ΔABC, czyli w środku przeciwprostokątnej. |OC|=R 2)

	1		1
|OE|=		|BC|=a, |OF|=		|AC|=b
	2		2

3) α=45^o⇔H=a, |ES|=a√2 β=60^o⇔ |FS|=2b W ΔSOF: (2b)²=a²+b²⇔a²=3b² a=b√3 4) W ΔSFB: a²+(2b)²=49 3b²+4b²=49⇔b=√7 i a=√21 5)W ΔABC: c²=(2a)²+(2b)² c²=(2√21)²+(2√7)² c²=4*21+4*7, c²=16*7, c=4√7

	1
6) |OC|=		c=2√7
	2

	1		1
PΔSOC=		H*|OC|=		*√21*2√7=√21*7
	2		2

P_ΔSOC=7√3 [ j²] ==============

PGinf: Kurde, myślałem że przecięcie środkowych podstawy wyznacza spadek wysokości dziękuję!