Podzielność Michał: Liczb całkowitych nieujemnych mniejszych od 2017, które są podzielne przez 3 lub 4 lecz nie są podzielne przez 5 jest

Adamm: |(A₃∪A₄)∩A₅^c| = |A₃∩A₅^c|+|A₄∩A₅^c|−|A₃∩A₄∩A₅^c| = |A₃|−|A₃∩A₅|+|A₄|−|A₄∩A₅|−|A₃∩A₄|+|A₃∩A₄∩A₅| = = 672−134+504−100−168+33 = 807

Jolanta: moż tak na począatek przez 3 a₁=3 r=3 an<2017 a_n=a₁+(n−1)r 3+(n−1)*3<2017 3+3n−3<2017 3n<2017

	1
n<672
	3

n=672

Adamm: |A_n| = [2017/n], gdzie A_n − zbiór liczb podzielnych przez n, mniejszych od 2017, [] − część całkowita

Jolanta: Adamm możesz mi wytłumaczyć dlaczego dodajesz 33 .Tak liczylam przez 4 a₁=4 r=4 n=504 liczby które dzielą sie przez 3 i 4 dzielą się przez 12 a₁=12 r=12 n=168 liczby które dzielą sie przez 3 i 5 dzielą się przez 15 a₁=15 r=15 n=134 liczby ,które dzielą się przez 4 i 5 dzielą się przez 20 a₁=20 r=20 n=100 liczby ,które dzielą sie przez 3 i 4 i 5 dzielą się przez120 a₁=120 r =120 n=12 672+504−168−134−100−12=762

Jolanta: ?

Jolanta: Czy ktoś może mi to wyjaśnić ?

Mila: Liczby ,które dzielą się przez 3 i 4 i 5 ⇔dzielą się przez 60 − jest ich 33

Jolanta: taaa u mnie 3*4*5=120 czyli powinniśmy odjąć 33 ?

Adamm: nie, dodać 33

Jolanta: dlaczego dodać ? Liczby mialy się dzielić przez 3 lub 4 ale nie przez 5.A te się dzielą

Mila: 1) |A₃∪A₄|=672+504−168=1008 2) |A_3,5∪A_4,5|=||A_3,5|+|A_4,5|−|A_3,5∩A_4,5|= =134+100−33=201 3) 1008−201=807

Adamm: To coś w rodzaju reguły włączeń i wyłączeń. Musisz je dodać, bo wcześniej odjęłaś za dużo

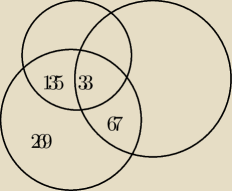
prosta: Proponuję diagram:

Jolanta: Dziekuję coś mnie zablokowało