Nigdy sie tego nie naucze Maciess: Spośród liczb 1,2,...,n (n≥3) losujemy kolejno bez zwracania dwie liczby. b) Dla jakich n prawdopodobieństwo tego, że różnica między większa a mniejszą liczbą jest równa

	1
2, jest większe od
	4

Nie wiem jak spytnie policzyć ilość zdarzeń sprzyjających

Blee: dla n≥5 1) wybieramy pierwszą liczbę z przedziału <3 ; n−2> 2) druga liczba musi być w przedziale <k−2 ; k+2> (gdzie k to wybrana liczba) i takich liczb jest dokładnie 4

	(n−4)*4
więc P(A1) =
	n*(n−1)

3) wybieramy pierwsza liczbę z puli: {2 ; n−1} 4) druga liczba musi być z puli {1, 3, 4} lub {n−3, n−2, n}

	2*3
więc P(A2) =
	n*(n−1)

5) wybieramy pierwszą liczbę z puli: {1 ; n} 6) druga liczba musi być z puli {2,3} lub {n−2, n−1}

	2*2
więc P(A3) =
	n*(n−1)

	4n − 16 + 6 + 4		4n−6
więc masz P(A) =		=
	n(n−1)		n(n−1)

dla n=3 i n=4 można szybko policzyć 'na paluszkach'

Blee: w końcu dla n=3 P(A) = 1 dla n=4

	|Ω| − 2
P(A) =		(bo tylko para (1,4) czy też (4,1) nie spełnia warunku)
	|Ω|

Maciess: Czym u ciebie jest zdarzenie A₂ i A₃?

Blee: A₁ <−−− opis przed tym (punkty (1) i (2) ) A₂ <−−− opis przed tym (punkty (3) i (4) ) A₃ <−−− opis przed tym (punkty (5) i (6) )

Maciess: Chyba analizowałem tak samo ale troszkę inaczej policzyłem. A₁ analizuje przypadek gdzie nie biore pod uwage dwóch koncowych liczb z przedziału np dla n=9 rozpatruje od <3,7> tak? Czyli dla wszystkich liczb z tego przedziału dopasuje 2 które spełniają warunek. Liczb jest w przedziale (n−4), a intreresująych mnie par (n−4)*2. Dlaczego u ciebie jest 4(n−4)?

Maciess: Aaa ty pewnie liczysz pary gdzie różnica liczb jest mniejsza bądź równa 2. A ma byc różnica dokładnie 2.

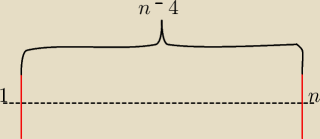
Maciess: Przedział <3,n−2> ma (n−4) elementów do każdego moge dopasować dwie liczby które się różnią o 2 i na pewno nalezą do przedziału. Czyli (n−4)*2 do tego mam pary {1,3},{2,4},{n,n−2},{n−1,n−3} czyli 4 przypadki

	2*(n−4)+4		2n−4
P(A)=		=
	n(n−1)		n(n−1)

Moze byc tak?

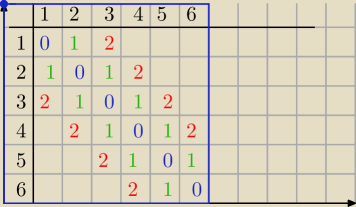
Mila: Ja zrobiłabym tabelę dla n=6 i uogólniła. Na przekątnej jest 6 (n) liczb − nie odpowiadają treści 1) Powyżej i poniżej przekątnej 2(n−1)liczb ( na ukos)− nie odpowiadają treści 2) Jeszcze raz powyżej i poniżej liczb : 2*(n−2)− odpowiadają treści |A|=2*(n−2) , n≥3 liczba zdarzeń sprzyjających zdarzeniu |a−b|=2

Blee: achhh ... różnica ma być DOKŁADNIE 2 No to mamy:

	(n−4)*2 + 4		2n−4
P(A) =		=
	n(n−1)		n(n−1)

Maciess: Super sposób i wychodzi to samo co w moim. Dziękuje