pierwiastkowanie liczb zespolonych
Cinek: 3√−27
pierwszy pierwiastek mi wyszedl −3*√2/2+3/2
i drugi mi wyszedl taki sam... jest to mozliwe?
3 gru 21:53
jc: Jednym z pierwiastków jest liczba −3.
Jeśli pomnożysz (−3) przez dowolny pierwiastek 3 stopnia z 1 nadal będziesz miał pierwiastek.
W ten sposób otrzymasz wszystkie 3 pierwiastki:
| | −1+i√3 | | −1−i√3 | |
−3, −3* |
| , −3* |
| |
| | 2 | | 2 | |
3 gru 22:00
Mila:
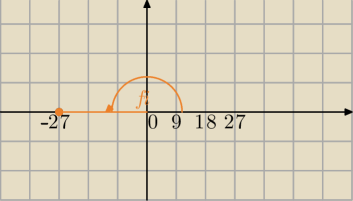
|−27|=27
φ=π
| | π+2kπ | | π+2kπ | |
zk=3√27*(cos |
| +i sin( |
| ), gdzie k∊{0,1,2} |
| | 3 | | 3 | |
| | π | | π | | 1 | | √3 | |
z0=3*(cos |
| +i sin |
| )=3*( |
| +i* |
| ) |
| | 3 | | 3 | | 2 | | 2 | |
z
1=3*(cosπ+i sin π)=−3
| | 5π | | 5π | | 1 | | √3 | |
z2=3*(cos |
| +i sin |
| )=3*( |
| −i* |
| ) |
| | 3 | | 3 | | 2 | | 2 | |
II sposób
z=
3√−27 /
3
z
3=−27
z
3+27=0
z
3+3
3=0
(z+3)* (z
2−3z+9)=0
z=−3 lub z
2−3z+9=0
Δ=−27=i
2*(
√27)
2
| | 3−3√3i | | 1 | | √3 | |
z1= |
| =3*( |
| − |
| ) |
| | 2 | | 2 | | 2 | |
3 gru 22:10