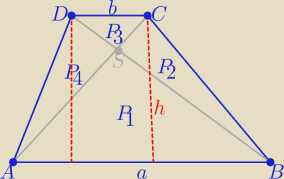
Proszę o pomoc Marcelinka: W trapezie ABCD (AB II CD) punkt S przecięcia przekątnych podzielił ten trapez na cztery trójkąty o polach oznaczonych jako: P1=Pabs, P2=Pbcs, P3=Pcds, P4=Pdas. 1. Udowodnij, że P2=P4. 2. Udowodnij, że P3/P2=P4/P1 3. Wiedząc, że pole trapezu ABCD wynosi P, a stosunek długości jego podstawy jest równy 2, oblicz P1, P2, P3, P4.

Eta:

	1
1/ P(ABD)=P4+P1=		a*h
	2

	1
P(ABC)=P1+P2)=		a*h
	2

to P₄+P₁= P₁+P₂ ⇒ P₄=P₂

	P1		a
2/		= k2 , k=		>0 −− skala podobieństwa ΔABS i DCS
	P3		b

oraz P₄=P₂=k*P₃ to P₄=P₂=√P₁*P₃ /²

	P4		P3
P4*P2=P1*P3 ⇒		=
	P1		P2

3/ k=2 P=P₁+P₂+P₃+P₄=k²*P₃+k*P₃+k*P₃+P₃ = (k+1)²*P₃

	P
to P3=
	(k+1)2

	P
dla k=2 P3=
	9

	2P
P2=P4= k*P3 =
	9

	4P
P1=k2*P3 =
	9

Marcelinka: Dziękuję bardzo!