twierdzenie sinusów i cosinusów cosinus: Środkowe AD i BE trójkąta ABC mają długości 9 i 12, a kąt między nimi zawarty ma miarę 120^o. Oblicz długości boków tego trójkąta.

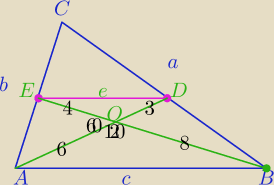
Mila: c=2e− odcinek łączący środki boków Δ środowe dzielą się w stosunku 2:1 licząc od wierzchołków Δ 1) W ΔDOE: e²=3²+4²−2*3*4*cos120^o e²=9+16+12 e=√37 c=2√37 ==== 2) w ΔAOE: |AE|²=4²+6²−2*4*6*cos60^o 3) W ΔBOD: |BD|²=3²+8²−2*3*8*cos60⁰ dokończ obliczenia

nie: nie