twierdzenie sinusów i cosinusów twierdzenie: Podstawami trapezu ABCD są odcinki AB i CD. Długość boku BC jest równa 6, a promień okręgu R

	sin|∡ABC|
opisanego na tym trapezie jest równy 5. Wiedząc, że		=1,6 oblicz pole P
	sin|∡BAC|

trapezu.

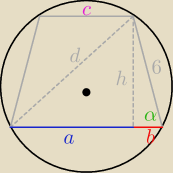
Blee: 1) skoro okrąg jest OPISANY na trapezie ... to mamy tutaj trapez równoboczny

	h   6
2)		= 1.6 −> d = 9.6
	h   d

	d		25
3) z tw. sinusów:		= 2*5 −> sinα =
	sinα		24

	h		25
4) sinα =		−> h =		= 6.25
	6		4

5) b² = 6² − h² −> b = .... 6) a² = d² − h² −> a = ... 7) c = a − 2b = ....

	a+c
8) P =		*h = ....
	2

Blee: i obyło się bez tw. cosinusów

twierdzenie: Oooo, dziękuję bardzo!

Blee: tyle że coś mam źle ... przecież sinus nie może wyjść ponad 1 proporcja sinusów musi być WIĘKSZA niż 1.6

Blee: a nie ... dobrze ... ja źle policzyłem

	d
sinα =		= 0.96
	10

więc h = 6*0.96 = 5.76 i teraz się zgadza

twierdzenie: Hmm, ale skoro h=6,25 to b²=6²−h² jest ujemne, czyż nie?

twierdzenie: Aaa, no właśnie.

twierdzenie: Chyba się zgubiłam. Od którego momentu jest błąd?

Bleee: Od (3).... źle wyznaczony sinα

Bleee: I blad w (7)... Oczywiście c = (a+b) − 2b I co dalej daje błąd we wzorze na pole trapezu Ogólnie P = a*h

twierdzenie: Rozumiem, bardzo dziękuję

twierdzenie: Jeszcze jedno pytanie w sumie. Dlaczego mam liczyć pole ze wzoru ah?

	a+b+c
Ogólnie licząc pole jako P=		* h dostaje P=44,2368 a w odpowiedziach mam P=44,26. Coś
	2

jest nie tak?

Blee: zapewne kwestia zaokrągleń zauważ, że: a+b = |AB| c = |CD| = a−b więc |AB| + |CD| = a+b+c = a+b +(a−c) = 2a dlatego wzór na pole trapezu będzie a*h

twierdzenie: Tyle, że jakby nie patrzeć, w żadnym miejscu nie zaokrąglałam wartości.

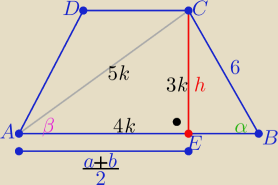
Eta: 1/ rys.

	6		3		3k
2/ R=5 z tw. sinusów w ΔABC		=2R ⇒ sinβ=		=
	sinβ		5		5k

	a+b
to |AE|=		= 4k
	2

więc P(trapezu)= 4k*3k= 12k² z treści zadania sinα= 1,6*0,6 = 0,96

	3k
i		=sinα ⇒ k= 2*0,96 ⇒ k=1,96
	6

P= 12*k²=..................,

Eta: sorry ma być k=1,92 ( P=44,24

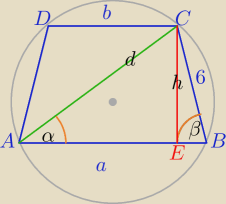
Mila: Trapez jest równoramienny R=5 1)

sinβ		8
	=		⇔5sinβ=8sinα
sinα		5

	6
2)		=2R⇔6=10*sinα
	sinα

sinα=0.6

d
	=10
sinβ

	d		d
d=10*sinβ⇔sinβ=		⇔5*		=8*0.6
	10		10

d=16*0.6=9.6 3) W ΔAEC:

	h		h
sinα=		⇔0.6=		⇔h=0.6*9.6
	d		9.6

h=5.76 cos²α=1−0.6²=0.64 cosα=0.8

	|AE|
cosα=
	d

	|AE|
0.8=		⇔|AE|=0.8*9.6=7.68
	9.6

	a+b
|AE|=
	2

P_ABCD=7.68*5.76=44.2368 =====================

Eta: