Rozkład Agata: Dane są niezależne zmienne losowe X, Y, Z. Zmienna losowa X ma rozkład dwupunktowy Bernoullego P(X = 0) = 1/4, P(X = 1) = 3/4, zmienna T ma rozkład jednostajny na przedziale [−1, 1], zaś Z ma rozkład jednostajny na przedziale [0, 2]. Znaleźć rozkład zmiennej W = XY + (1 − X)Z. Dla dówch zmiennych moge korzystac ze spolotu gestosci a co w tym przypadku?

Blee:

	⎧	Y dla X=1
W =	⎩	Z dla X=0

Blee: tfu W={3Y/4 dla X=1 & Z/4 dla X=0}

Blee:

	⎧	3Y/4 dla X=1
W=	⎩	Z/4 dla X=0

Agata: Jak to policzyłes? Zalezy mi na wskazówkach

Agata:

Blee: zapomnij o tym co napisałem −−− to jest idiotyzm człeka który ledwie się obudził

Adamm:

	3		1
P(W≤t) = P(W≤t | X = 1) + P(W≤t | X = 0) =		P(Y≤t)+		P(Z≤t)
	4		4

P(W≤t) = 0 dla t≤−1

	3		t+1
=		*		dla −1≤t≤0
	4		2

	3		t+1		1		t
=		*		+		*		dla 0≤t≤1
	4		2		4		2

	3		1		t
=		+		*		dla 1≤t≤2
	4		4		2

= 1 dla t≥2

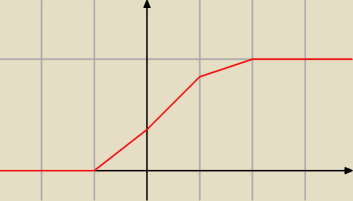
Adamm: dystrybuanta

Agata: A tam nie powinno byc 4/3 oraz 4? w prawdopodobieństwie we wzorze warunkowym?

Adamm: P(W≤t) = P(W≤t | X=0)P(X=0) + P(W≤t | X=1)P(X=1) tak powinno być, reszta jest ok

Agata: super dziękuje!