pochodne i monotoniczność funkcji gracjan - pogromca zadań :-): Witam mam pytanie oto funkcja:

	x2+6x+10
f(x) =
	x+3

Liczymy pochodną:

	x2+6x+8
f'(x)=
	(x+3)2

Określamy monotoniczność funkcji: Miejsca zerowe pochodnej: x₁ = −4 x₂ = −2 I teraz mam pytanie bo na początku wyznaczyłem monotoniczność jako: f(x) rośnie dla x∊(−∞; −4) ∨ (−2; ∞) f(x) maleje dla x∊(−4; −3) ∨(−3; −2) A z odpowiedzi wynika że powinienem napisać: f(x) rośnie dla x∊(−∞; −4> ∨ <−2; ∞) f(x) maleje dla x∊<−4; −3) ∨(−3; −2> Więc dlaczego uwzględniam także miejsca zerowe Z tego rozumowania wynika że dla x = −4 i x = −2 funkcja rośnie i maleje na raz?! Jaki w tym sens?! Dzięki za pomoc i pozdrawiam!

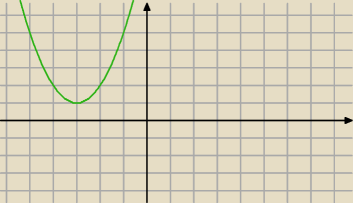
Jerzy: Nie wiem, czy ta pochodna jest dobrze policzona. Popatrz na wykres licznika pochodnej. Skoro pochodna jest stale dotania, to funkcja stale rośnie.

Jerzy: Skąd miejsca zerowe pochodnej ? (−2)² + 6*(−2) + 10 = 4 − 12 + 10 = 2 ≠ 0

Jerzy: Pokaż , jak liczyłeś tą pochodną ?

gracjan - pogromca zadań :-):

	(2x+6)(x+3)−(x2+6x+10)
f'(x)=
	(x+3)2

licznik: x²+6x+8 = 0 Δ=36−32=4=2² x₁=−4 x₂=−2

gracjan - pogromca zadań :-): Użyłeś złego wzoru Jerzy

gracjan - pogromca zadań :-): i wyliczyłeś ekstremum

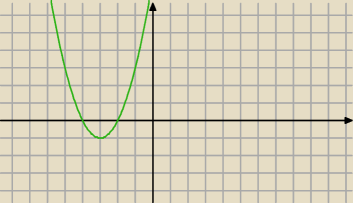
Jerzy: Pomyłka .... maximum dla : x = − 4 , minimum dla: x = − 2

Jerzy: Tam, gdzie pochodna dodatnia funkcja rośnie i odwrotnie.

gracjan - pogromca zadań :-): Dlaczego rośnie i maleje NARAZ dla miejsc zerowych?

Maciess: Pasuje na wykresie uwzględnić dziedzine

gracjan - pogromca zadań :-): dziedzine widac na pierwszy rzut oka R\{−3}, uwzględniłem to w zakresach. Odpowie mi ktoś na moje pierwotne pytanie

Maciess: A podstaw sobie te wartości, sprawdź z definicji i chyba się domyślisz czemu

gracjan - pogromca zadań :-): A to chyba już rozumiem, jeśli podstawię np. m = f(−4) − f(−5) to m jest > 0. z kolei jeśli podstawię m = f(−3) − f(−4) to m < 0.

Maciess: Jeśli jest ekstremum w tym punkcie to oczywiście, że uwzględniasz w przedziale. Na tym konkretnym przykładzie Wartości funkcji rosną od −∞, a w x=−4 jest maksimum lokalne, to znaczy że każda wartość funkcji na lewo od −4 będzie mniejsza od tej największej w x=−4.

Jerzy: Słyszałeś coś o asymptocie pionowej funkcji ?