nierówność
marynarz05: (x+5)(x−3)3(2−x)2≥0
coś mi nie wychodzi... liczę ze wzorów skróconego mnożenia, mógłby ktoś to rozpisać?
30 lis 15:19
Jerzy:
Zauważ,że (2 − x)2 ≥ 0 dla dowolnego x.
Musi zatem być: (x + 5)((x − 3)3 ≥ 0
30 lis 15:22
30 lis 15:23
Mila:
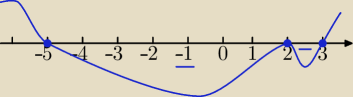
A po co wzory tutaj ? Masz postać iloczynową i to jest już luksus!
(x+5)(x−3)
3*(2−x)
2≥0
x=−5 lub x=3 (potrójnie) lub x=2 (podwójnie)
x∊(−
∞,−5>∪<3,
∞>∪{2}
30 lis 18:44
PW: Jestem zwolennikiem jeszcze prostszego rozwiązania:
− nierówność jest prawdziwa dla
(1) x∊{−5, 2, 3}
− dla pozostałych x dzielimy obie strony przez dodatni iloczyn (x−3)2(2−x)2 otrzymując
nierówność równoważną
(2) (x+5)(x−3) ≥ 0.
Ilustracja to parabola dla nierówności (2) − rozwiązania to x∊(−∞, −5>∪<3,∞) oraz dodatkowo {2}
− rozwiązanie z (1).
Wolę coś takiego, żeby nie wpadać w żargon "odbijania się lub nie" węża od osi w poszczególnych
miejscach zerowych..
30 lis 22:06
 Zastosuj 'wezyka' : https://matematykaszkolna.pl/strona/142.html
Zastosuj 'wezyka' : https://matematykaszkolna.pl/strona/142.html
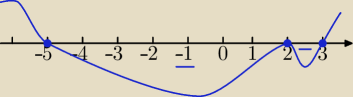 A po co wzory tutaj ? Masz postać iloczynową i to jest już luksus!
(x+5)(x−3)3*(2−x)2≥0
x=−5 lub x=3 (potrójnie) lub x=2 (podwójnie)
x∊(−∞,−5>∪<3,∞>∪{2}
A po co wzory tutaj ? Masz postać iloczynową i to jest już luksus!
(x+5)(x−3)3*(2−x)2≥0
x=−5 lub x=3 (potrójnie) lub x=2 (podwójnie)
x∊(−∞,−5>∪<3,∞>∪{2}