Funkcja z wartoscia bezwzgledna
xxx: f(x) = |x−1| − |x+1| + 1
Rozpisalem sobie te wartosci bezwzgledne z definicji:
{x−1, x−1 ≥ 0, x ≥ 1
|x−1| = {−x−1, x−1 < 0, x < 1
{x+1, x ≥ −1
|x+1| ={−x−1, x < −1
Teraz rysuje sobie wykres i powinienem rozwiazac w trzech przedzialach: 1) x < −1 2) x ∈
<−1; 1> 3) x ≥1
I teraz nie wiem czy mam bledy w zeszycie czy po prostu zle cos licze, ale ostatecznie te
funkcje mi zle wychodza. Moglby ktos rozwiazac, zebym mogl porownac?
30 lis 14:08
Jerzy:
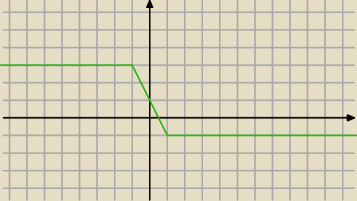
30 lis 14:12
PW: Od razu f(x):
− na zbiorze (−∞,1)
f(x)=−(x−1)−(−(x+1))+1=−x+1+x+1+1=3
− na zbiorze <−1, 1>
f(x)=−(x−1)−(x+1)+1 =
itd.
30 lis 14:17
xxx: no dobrze, juz chyba wiem co mam zle, ale mam jeszcze jedno pytanie.
rozwiazuje sobie w drugim przedziale czyli x ∈ <−1;1> cos takiego:
f(x) = −x +1 − (x+1) + 1
moje pytanie brzmi: czy jak mam wyrazenie "−(x+1)" to ten nawias jest konieczny? bo wtedy
zmieniamy wszystkie znaki w nawiasie, wydawalo mi sie ze przepisywalo sie po prostu wyrazenie
bez zmian czyli "x+1", bez tego minusa na poczatku
30 lis 14:19
Jerzy:
Tak, bo: − x + 1 ≠ −(x + 1)
30 lis 14:21
PW: −(x+1)=−x−1 (można sobie to wytłumaczyć, że mnożysz (−1)(x+1), a więc wynik to −1x−1•1=−x−1)
30 lis 14:25
