nierówność wartość bezwzględna
Piotr:
| | 3 | | 3 | |
1) 2− |
| ≥4 v 2) 2− |
| ≤−4 |
| | x | | x | |
Teraz w rozwiązaniu mam, że dla dla tego pierwszego x>0 a dla drugiego x<0, dlaczego?
29 lis 20:07
Piotr: Oczywiście dalej jest pomnożone przez x i sprawdzone czy zawiera się w przedziale. Chodzi mi o
to czy mógłbym założyć odwrotnie, dla pierwszego x<0 a drugiego x>0, i dlaczego tak a nie
inaczej?
29 lis 20:10
ABC: ale przecież druga nierówność jest spełniona na przykład dla x=1/2 bo wtedy masz równość 6=6
coś nie tak z tym rozwiązaniem
29 lis 20:11
Leszek: np. 6 ≤ 3/x ⇔ 6 −3/x ≤ 0 ⇔ (6x−3)/x ≤ 0 ⇔ (6x−3)x ≤ 0 ⇒ x= ........
29 lis 20:15
Piotr: Wróć. Dla pierwszej mam, że x<0 a dla drugiego x>0. Chodzi o to, że jak postawię w pierwszym
x>0 to nie będzie miało rozwiązania?
:
29 lis 20:20
Piotr: Inaczej, czy jak zrobię tak, że pierwszy przypadek rozpatrzę dla x>0 a potem x<0 a potem drugi
przypadek tak samo, i sprawdzę z tymi założeniami, to też będzie poprawne?
29 lis 20:23
Leszek: Piotr , a skad to masz , ze x > 0 lub x< 0 ? ?
29 lis 20:23
Piotr: Takie założenie, żebym mógł pomnożyć przez x i mieć pewność czy znak się zmienił czy też nie.
29 lis 20:34
Leszek: Jest to zalozenie z" sufitu" rownie dobrze mozna przyjac odwrotnie i co wyniknie ?
Pokazalem Ci jak to nalezy zrobic ( 6x−3)x≤ 0 ⇒ x = (−∞ ,0) ∪ [ 0,5 ; ∞)
Podabnie druga nierownosc i suma przedzialow bedzie ostatecznym rozwiazaniem !
Popatrz do podrecznika ! ! !
29 lis 20:40
Mila:
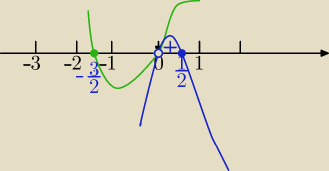
x≠0
(2x+3)*x≤0 lub (−6x+3)*x≥0
| | 3 | | 1 | |
x=0, x=− |
| , x= |
| , x=0 |
| | 2 | | 2 | |
| | 3 | | 1 | |
x∊<− |
| ,0) lub x∊(0, |
| > suma przedziałów: |
| | 2 | | 2 | |
|| sposób
|2x−3|≥4*|x| /
2
4x
2−12x+9≥16x
2
−12x
2−12x+9≥0 /:(−3)
4x
2+4x−3≤0
Δ=64
==================
29 lis 20:41
Piotr: Leszek, rozumiem twoje rozwiązanie i dzięki.
"Takie założenie, żebym mógł pomnożyć przez x i mieć pewność czy znak się zmienił czy też nie."
Oczywiście tak mi się wydaje, bo to nie moje rozwiązanie, więc mogę się tylko domyślać, dlatego
próbowałem to zrozumieć

29 lis 20:43
Piotr: Dzięki Mila

29 lis 20:44
 x≠0
x≠0

