użycie wzorów viet'a i napisanie założeń:
Michał: Prosiłbym tutaj o użycie wzorów viet'a i napisanie założeń:
a)Dla jakich wartości parametru m nierówność (m²−1)x²+2(m−1)x+2>0
jest spełniona dla każdego x∈R?
b) Dla jakich wartości parametru m funkcja przyjmuje wartości dodatnie dla każdego x∈R
f(x)=(m²+4m−5)x²−2(m−1)x+2
29 lis 17:01
ICSP: a) :
1o a = b = 0 ∧ c > 0
2o a > 0 ∧ Δ < 0
b) :
1o a = b = 0 ∧ c > 0
2o a > 0 ∧ Δ < 0
29 lis 18:09
Michał: a)
1o
a =0 b = 0 ∧ c > 0
a:
m
2−1=0
m
2=1
m=−1 v m=1
m≠0 sprzeczne przypadek niemożliwy
b:
2(m−1)=0
m−1=0
m=1
m≠0 sprzeczne przypadek niemożliwy
c:
2>0
2o a > 0 ∧ Δ < 0
a: Δ=(2m−2)
2 −4 2 (m
2−1)
m
2−1>0 Δ= 4m+4 − 8m
2−8
m
2>1 Δ=4m−4<0
m>−1 v m>1
m∊ (−
∞,−1) U (1,
∞)
czy dobrze rozwiązałem

? czy przy delcie trzeba coś dopisać?
29 lis 19:25
Blee:
Michał −−− nie bardzo kumam:
1o
a =0 b = 0 ∧ c > 0
a:
m
2−1=0
m
2=1
m=−1 v m=1
m≠0 sprzeczne przypadek niemożliwy
Niby dlaczego to daje sprzeczność

niech m=1 wtedy a=0 i b=0 i c=2 > 0
29 lis 19:30
Michał: a no tak

a w drugim przypadku wszystko jest ok czy coś brakuje?
29 lis 19:33
Blee:
druga sprawa ... (2m−2)
2 = 4m+4

natomiast −4*2(m
2−1) = −8m
2 − 8

Coś tutaj widzę nową matematykę ktoś tworzy
29 lis 19:33
Michał: faktycznie źle z notatnika spisałem dobrze że czuwasz

29 lis 19:47
Michał: b)
a>0
m2+4m−5>0
m2+4m>5
m(4+m)>0
m>0 v m>−4
Δ=(−2m+2)2−4*2(m2+4m−5)
Δ=4m2+4−8(m2+4m−5)
Δ=4m2+4−8m2−32m+40
Δ= −4m2−32m+44
Δ<0
m∊ (−∞,−4) U (0,∞)
czy dobrze rozwiązałem?
29 lis 20:05
Bleee:
A czemu nie rozwiazales dla jakim m będzie zachodzilo Δ<0

No i nadal (a) nie jest rozwiązane dobrze
29 lis 21:05
Bleee:
I znowu.... Cholera niby od kiedy (−2m +2)
2 = 4m
2 + 4

Skąd taki pomysł

Spójrz sobie na wzory skróconego mnożenia

29 lis 21:07
Bleee:
Widzę że masz spore braki
29 lis 21:07
Michał: a)
Δ= (2m−2)2−4*(m2−1)2
Δ= 4m2−8m+4−8m2−8
Δ= −4m2−8m−4. <0
−4m2−8m−4<0
−4m2−8m<4
−4m(m+2)<4
m+2>−1
m>−3
29 lis 21:32
Blee:
a gdzie 'm' się zgubiło

29 lis 21:45
Blee:
NADAL źle wyznaczona Δ
29 lis 21:46
Michał: W takim razie jak wyglada poprawna Δ?
29 lis 21:52
Michał:
Czy tak? Nie wiedziałem że mam − przed 8
Δ= 4m2−8m+4−8m2+8
Δ= −4m2−8m+12<0
A to m to w jaki sposób wyznaczyć ?
29 lis 21:56
Mila:
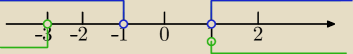
a)Dla jakich wartości parametru m nierówność
(m²−1)x²+2(m−1)x+2>0 jest spełniona dla każdego x∈R?
1) m
2−1>0 i Δ<0
a) m
2−1>0
(m−1)*(m+1)>0
m<−1 lub m>1
b)
Δ=4(m−1)
2−4*2*(m
2−1)=4(m
2−2m+1)−8m
2+8
Δ=4m
2−8m+4−8m
2+8
Δ=−4m
2−8m+12
−4m
2−8m+12<0
Δ
m=64−4*12*(−4)=64+192=256
| | 8−16 | | 8+16 | |
m= |
| =1 lub m= |
| =−3 |
| | −8 | | −8 | |
Parabola jest skierowana w dół
m<−3 lub m>1
Część wspólna (a i b)
f(x)=(m²−1)x²+2(m−1)x+2>0 dla każdego x∊R⇔m∊(−
∞,3)∪(1,
∞)
===========================================
29 lis 22:15
 ? czy przy delcie trzeba coś dopisać?
? czy przy delcie trzeba coś dopisać?
 niech m=1 wtedy a=0 i b=0 i c=2 > 0
niech m=1 wtedy a=0 i b=0 i c=2 > 0
 a w drugim przypadku wszystko jest ok czy coś brakuje?
a w drugim przypadku wszystko jest ok czy coś brakuje?
 natomiast −4*2(m2−1) = −8m2 − 8
natomiast −4*2(m2−1) = −8m2 − 8  Coś tutaj widzę nową matematykę ktoś tworzy
Coś tutaj widzę nową matematykę ktoś tworzy

 No i nadal (a) nie jest rozwiązane dobrze
No i nadal (a) nie jest rozwiązane dobrze
 Skąd taki pomysł
Skąd taki pomysł Spójrz sobie na wzory skróconego mnożenia
Spójrz sobie na wzory skróconego mnożenia

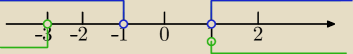 a)Dla jakich wartości parametru m nierówność
(m²−1)x²+2(m−1)x+2>0 jest spełniona dla każdego x∈R?
1) m2−1>0 i Δ<0
a) m2−1>0
(m−1)*(m+1)>0
m<−1 lub m>1
b)
Δ=4(m−1)2−4*2*(m2−1)=4(m2−2m+1)−8m2+8
Δ=4m2−8m+4−8m2+8
Δ=−4m2−8m+12
−4m2−8m+12<0
Δm=64−4*12*(−4)=64+192=256
a)Dla jakich wartości parametru m nierówność
(m²−1)x²+2(m−1)x+2>0 jest spełniona dla każdego x∈R?
1) m2−1>0 i Δ<0
a) m2−1>0
(m−1)*(m+1)>0
m<−1 lub m>1
b)
Δ=4(m−1)2−4*2*(m2−1)=4(m2−2m+1)−8m2+8
Δ=4m2−8m+4−8m2+8
Δ=−4m2−8m+12
−4m2−8m+12<0
Δm=64−4*12*(−4)=64+192=256