geometria analityczna bbxx: Prosta k o równaniu y=ax+b, gdzie a∊(0,1), przechodząca przez punkt P(−3,2) przecina dodatnią półoś osi OY w punkcie A, a ujemną półoś osi OX w punkcie B.Pole trójkąta AOB, gdzie O=(0,0) jest równe 12,5. a) wyznacz równanie kierunkowe prostej k

	4		10
(wyznaczyłam, y=		x +		)
	9		3

b) Prosta m, która jest obrazem prostej k w jednokładności o środku O(0,0) i skali k=6, przecina oś OY w punkcie D, zaś oś OX w punkcie C. Oblicz pole trapezu ADCB. Nie umiem zrobić drugiego podpunktu, myślałam, że można wyznaczyć długość przekątnej AD i BC i z pola na dowolny czworokąt (bo kąt między przekątnymi byłby prosty) wyliczyć to pole trapezu, ale to nie wychodzi. Czy ktoś mógłby to dokładnie wytłumaczyć?

K: Odległość między prostymi to wysokość trapezu. Po co Ci przekątne?

K: ... albo obliczasz pole trójkąta COD i odejmujesz pole trójkąta AOB...

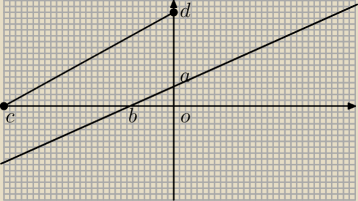
bbxx: Ale wyobrażam sobie to w ten sposób, że obrazem punktu A jest punkt D, a obrazem punktu B jest punkt C, a wtedy odejmowanie od pola COD pola AOB chyba nie ma sensu. Mógłbyś to rozrysować albo wytłumaczyć dokładniej?

K: 450−12,5=437,5 pole trapezu

K: Zgadza się, obrazem A jest D, a B− C. Jakie współrzędne ma D i C?

K:

bbxx: Ok, już rozumiem, w czym zrobiłam błąd. Rysowałam ten wykres dla k=−6, a wtedy wszystko odbijało się na drugą stronę. Dziękuję! Załapałam w końcu