Oblicz P(A) Maciess: Oblicz P(A) jeśli P(B)=2P(B')

	1
P(A|B)=
	5

	3
P(A|B')=
	5

I nie wiem czy dobrze myśle, ale czy P(A) to będzie po prostu P(A∩B)∪P(A∩B') ?

Mila: Co oznacza zapis: P(A|B) warunkowe prawd. , czy prawd. różnicy zbiorów?

Blee: P(A) = P(A|B)*P(B) + P(A|B')*P(B') (patrz prawdopodobieństwo całkowite)

Maciess: Mila warunkowe Wynik wychodzi taki sam jak u mnie to kwestia przypadku w tym zadaniu czy...

Eta:

	2		1
P(B)=2P(B') ⇒ P(B)=		, P(B')=
	3		3

i jak napisał [P[Blee] .................

	1		2		3		1		1
P(A)=		*		+		*		=
	5		3		5		3		3

=====

Mila:

	2
P(B)=
	3

	1
P(B')=
	3

	1		2		2
P(A∩B)=		*		=
	5		3		15

	3		1		3
P(A∩B')=		*		=
	5		3		15

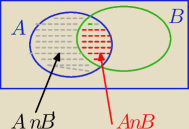
	1
P(A)=P(A∩B)+P(A∩B')==
	3

Mila:

	P(A∩B)
P(A/B)=
	P(B)

Eta:

	1
lub P(A)= P(A∩B)+P(A∩B') =
	3

	1		2		3		1
bo P(A∩B)=		*		, P(A∩B')=		*
	5		3		5		3

Maciess: o dziękuje, graf rozwiał moje wątpliwości Tak sobie wyobrażałem te zbiory, ale nie byłem pewien. Musze częściej wspomagać się rysunkiem