styczna do okręgu julka.wawrzyniak: Okrąg przechodzi przez punkt A(4,1), zaś jego środek należy do prostej k: x−y=0. Wiedząc, że okrąg ten jest styczny do prostej l: y−5=0, wyznacz jego równanie.

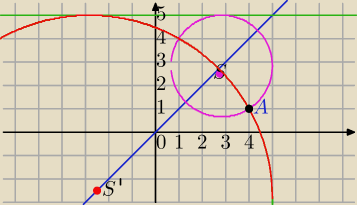
Mila: S=(a,a)∊k, A=(4,1) l: y−5=0 1) |AS|=d(S,l)=|a−5| √(a−4)²+(a−1)²=|a−5| a²−8a+16+a²−2a+1=a²−10a+25, a²=8 a=2√2 lub a=−2√2 S=(2√2,2√2) lub S'=(−2√2,−2√2) 1)S=(2√2,2√2) , A=(4,1) r²=(2√2−4)²+(2√2−1)² r²=4*(√2−2)²+8−4√2+1 r²=4*(2−4√2+4)+9−4√2 r²=33−20√2 Równanie okręgu: (x−2√2)²+(y−2√2)²=33−20√2 lub 2) S'=(−2√2,−2√2) r²=(−2√2−4)²+(−2√2−1)² r²=33+20√2 Równanie okręgu: (x+2√2)²+(y+2√2)²=33+20√2 ==============================