 |z−2−i|>|z−3|
z=x+iy, x,y∊R
|x+iy−2−i|>|x+iy−3|
|(x−2)+i*(y−1)|>|(x−3)+iy|
√(x−2)2+(y−1)2>√(x−3)2+y2 /2
x2−4x+4+y2−2y+1>x2−6x+9+y2
−4x+4−2y+1>−6x+9
−2y> −2x+4 /:(−2)
y<x−2
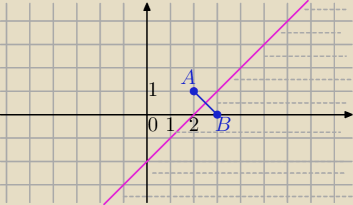
obszar pod prostą y=x−2
II sposób
Symetralna odcinka o końcach A=(2,1) i B=(3,0)
(x−2)2+(y−1)2=(x−3)2+y2
y=x−2
Wybierasz obszar , sprawdzając dla jednego punktu np. (0,1) lub (3,0) .
|z−2−i|>|z−3|
z=x+iy, x,y∊R
|x+iy−2−i|>|x+iy−3|
|(x−2)+i*(y−1)|>|(x−3)+iy|
√(x−2)2+(y−1)2>√(x−3)2+y2 /2
x2−4x+4+y2−2y+1>x2−6x+9+y2
−4x+4−2y+1>−6x+9
−2y> −2x+4 /:(−2)
y<x−2
obszar pod prostą y=x−2
II sposób
Symetralna odcinka o końcach A=(2,1) i B=(3,0)
(x−2)2+(y−1)2=(x−3)2+y2
y=x−2
Wybierasz obszar , sprawdzając dla jednego punktu np. (0,1) lub (3,0) .
