Nierówności kwadratowe. diunaj: Jak rozwiązać takie nierówności kwadratowe? Proszę o wytłumaczenie krok po kroku. z góry dziękuję za pomoc. a)√x−2 < 8− x b) √x + 3 > 9 − x

diunaj: up

diunaj: up

diunaj: up

diunaj: up, cholera czy to jest aż tak trudne że nikt nie umie tego rozwiązać?x/

walet: Nie, to jest bardzo proste i aż dziwne, ze sam tego nie umiesz rozwiązać, cholera

diunaj: No to skoro jest to takie proste, to zrób i udowodnij

k4r: podnieś wszystko do kwadratu, i policz (liczba pod pierwiastkiem jest podniesiona do potęgi 1/2)

diunaj: Eh, dobra, tłumacze po kolei w czym jest problem: √x −2 < 8 − x Dziedzina: x − 2 ≥ 0 ⇒ x ≥ 2 ⇒ x ∊<2; + ∞) √x −2 < 8 − x / ()² x − 2 < 64 − 16x + x² x² − 17x + 66 > 0 Δ = 25 √Δ = 5 x₁ = 6 , x₂ = 11 Czyli x∊(−∞; 6)∪(11;+∞) ∧ x ∊ D_r ⇒ x∊<2;6)∪(11;+∞) A ma wyjść tylko x ∊ <2;6) WTF?

Godzio: na początku trzeba ustalić dziedzine : a) x−2≥0 x≥2 √x−2<8−x /² x−2 < 64 − 16x + x² 0 < x² − 17x + 66 Δ = 25 x₁ = ... x₂ = ... Odp : uwzględnij dziedzine

diunaj: Generalnie rzecz biorąc, dobrze wiem jak to liczyć, ale nie wychodzi ;x A cwaniakom i geniuszom takim jak "walet" to ja z góry dziękuję za niezabieranie głosu.

diunaj: Godzio, no pokazałem, że robie dokładnie tak samo, ale to k****wo nie chce wyjść, bo w odpowiedziach jest co innego...

Godzio: jak na moje oko to błędu tutaj nie widze może w odpowiedzi się pomylili ? sprawdz czy dobrze przepisałeś zadanie

diunaj: na pewno dobrze. I to samo dzieje sie w kolejnym przykładzie, wynik wychodzi mi tylko "po części" dobrze. Ofc uwzględniam za każdym razem dziedzinę.

Godzio: nie mam pojęcia skąd oni to wzieli

diunaj: No widzisz, ale najśmieszniejsze jest to... że mają racje. Bo gdy do nierówności podstawisz coś z tej drugiej (błędnej) części przedziału, to nie wychodzi. Czyżby podczas rozwiązywania tego rodzaju nierówności był jeszcze jakiś warunek?

Godzio: być może można dać jeszcze taki warunek √x −2 < 8 − x skoro ma być to spełnione to 8 − x > 0 bo √ x ≥0 −x > −8 x<8 ale głowy nie dam

diunaj: Haha, a wiesz że tez tak myślałem? I nawet tak zrobiłem wpierw, ale w takim wypadku w tym drugim przykładzie sytuacja musiałaby być podobna, a gdy i w nim tak zrobię to już kompletne bzdury wychodza, czyli to nie to x/

bla bla: do dziedziny należy jeszcze 8−x>0 x<8 ponieważ pierwiastek nie może byc liczbą ujemną.

justka: Trzeba poprawić założenia 1. x−2≥0 ⇒x∊<2; +∞) 2. 8−x≥0 ( jeśli po prawej stronie nierówności będzie liczba ujemna to otrzymamy sprzeczność − po lewej zawsze mamy liczbę nieujemną) 1 i 2 ⇒x∊<2;8> porównując teraz to z rozwiązaniem x∊(−∞; 6)∪(11;+∞) i x∊<2;8> ⇒x<2;6)

diunaj: No dobra, czyli jednak to jest to. A co z tym drugim przykładem? Powinno wyjść (6;+∞)

Godzio: bo w drugim pierwiastek > od liczby więc tu takiego założenia nie potrzeba

diunaj: no ale jak w tym drugim również czegos nie założysz, to znowu błędny wynik wychodzi chociaż liczę na pewno dobrze, bo już tyle razy to sprawdzałem...

justka: Rozpatrz dwa przypadki: I. 9− x <0 II. 9 − x ≥0

diunaj: √x+3 > 9 − x /()² D_r = {x:x ∊ <−3;+∞)} x + 3 > 81 − 18x + x² x² − 19x + 78 < 0 Δ = 49 √Δ = 7 x₁ = 6 x₂ = 13 I to za żadne skarby nie da tego (6;+∞)...

diunaj: Justka, a możesz wytłumaczyć, z czego wynika potrzeba rozpatrywania tych dwóch przypadków? Bo jakoś tego nie widze...

diunaj: Nawet po rozpatrzeniu tych dwóch przypadków, w dalszym ciągu wychodzi jakiś kompletnie oderwany od rzeczywistości wynik.WTF?!

justka: I. 1. 9−x <0 ⇒x∊(9;+∞) 2. x+3≥0 ⇒x∊<−3;+∞) 1 i 2 ⇒x ∊(9: +∞) dla x ∊(9: +∞) wyrażenie po prawej stronie nierówności jest zawsze ujemne a po lewej jest dodatnie czyli ta nierówność jest spełniona dla każdego x ∊(9: +∞) II. 9−x ≥0 i x+3≥0 ⇒ <−3; 9> √x+3 > 9 − x /()² x + 3 > 81 − 18x + x²1 x² − 19x + 78 < 0 Δ = 49 √Δ = 7 x1 = 6 x2 = 13 x∊(6; 13) i x ∊<−3; 9> ⇒x∊(6; 9> I lub II⇒ x∊(6; +∞)

diunaj: Aaa, w ten sposób... rozumiem... za CHOLERĘ nie rozumiem skąd się wziął ten drugi przypadek, możesz trochę bardziej łopatologicznie to wytłumaczyć (wiem, jestem ciężkim przypadkiem, ale naprawdę chciałbym to pojąć...)

justka: jeżeli po jednej stronie nierówności masz liczbę ujemną to nie możesz podnieść obu stron nierówności do kwadratu (np 3>−5 jeśli podniesiesz to do kwadratu to otrzymasz 9> 25 a to jest bzdura) dlatego musisz rozpatrywać dwa przypadki

diunaj: <załamka> Eh, no jasne... ale ze mnie głupek ;x Dzięki serdeczne za pomoc

justka: cieszę się że mogłam pomóc

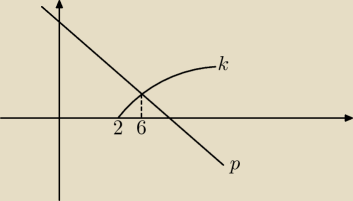
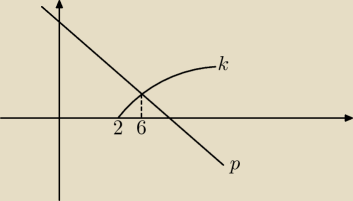walet: Ech. krzywa k; y = √x − 2 prosta y = −x + 8 Gdzie krzywa jest pod prostą?