planimetria
ppp: W trójkącie prostokątnym ABC o kącie prostym przy wierzchołku C. Długość wysokości CD, długość
środkowej CE i długość przeciwprostokątnej AB tworzą w podanej kolejności ciąg geometryczny o
iloczynie wyrazów równym 64. Oblicz stosunek pola koła wpisanego w trójkąt CDE do pola koła
opisanego na trójkącie ABC.
25 lis 17:33
Eta:
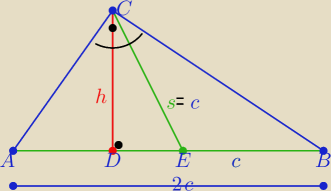
....... rys i oznaczenia
z treści zadania h,c,2c −−− tworzą ciąg geometryczny
to c
2=2hc ⇒c=2h to 2c=4h
h*2h*4h=64 ⇒ h
3=8 ⇒ h=2 to c=4 i 2c=8
więc |DE|= 2
√3
w ΔABC R=c=4 to P
k opisanego= ...........
w ΔDEC 2r= h+c+|DE| ⇒ r=
√3−1
P
k wpisanego = ..............
podaj odpowiedź...........
25 lis 17:59
ppp: Dziękuję za pomoc.
25 lis 18:04
Eta:

25 lis 18:20
Spioch: Eta dlaczego 2r = h+c+|DE|?
25 lis 18:43
Eta:
Chochlik

Ma być :
2r=h+c
−|DE|
25 lis 18:47
Blee:
Etuś ... raczej 2r = h
−c
+|DE|

25 lis 18:49
Spioch: Eta a z czego wynika ta zależność?
25 lis 18:51
Eta:
Masz rację Blee
2r= h+|DE|−c
25 lis 18:53
Eta:
@
Blee
Jak to dobrze ,że wszędzie Cię pełno

Aż strach się brać za jakieś zadanie ...

25 lis 18:54
Eta:
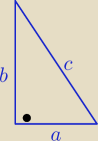
@
Spioch
25 lis 18:55
Blee:
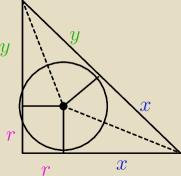
A kojarzysz taki oto rysunek

To z tego wyznacz ile równe jest 2r

25 lis 18:56
Spioch: Dzięki!
25 lis 18:59
Eta:
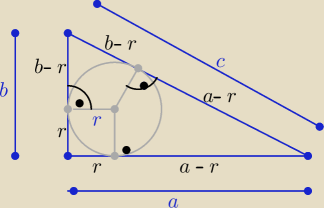
c= a−r+b−r ⇒ 2r= a+b−c
25 lis 19:01
Eta:
A teraz "spadam" .... niech
Blee się "produkuje

25 lis 19:03
Blee:
ja zaczynam oglądać mecz, więc też spadam

Zresztą ja nie mam takiego zacięcia co Ty Etuś w 'produkowaniu się'

Ja jednak leniuch jestem

25 lis 19:04
 ....... rys i oznaczenia
z treści zadania h,c,2c −−− tworzą ciąg geometryczny
to c2=2hc ⇒c=2h to 2c=4h
h*2h*4h=64 ⇒ h3=8 ⇒ h=2 to c=4 i 2c=8
więc |DE|= 2√3
w ΔABC R=c=4 to Pk opisanego= ...........
w ΔDEC 2r= h+c+|DE| ⇒ r=√3−1
Pk wpisanego = ..............
podaj odpowiedź...........
....... rys i oznaczenia
z treści zadania h,c,2c −−− tworzą ciąg geometryczny
to c2=2hc ⇒c=2h to 2c=4h
h*2h*4h=64 ⇒ h3=8 ⇒ h=2 to c=4 i 2c=8
więc |DE|= 2√3
w ΔABC R=c=4 to Pk opisanego= ...........
w ΔDEC 2r= h+c+|DE| ⇒ r=√3−1
Pk wpisanego = ..............
podaj odpowiedź...........

 Ma być :
2r=h+c−|DE|
Ma być :
2r=h+c−|DE|

 Aż strach się brać za jakieś zadanie ...
Aż strach się brać za jakieś zadanie ... 
 @Spioch
@Spioch
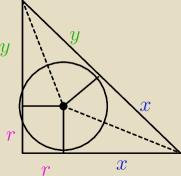 A kojarzysz taki oto rysunek
A kojarzysz taki oto rysunek  To z tego wyznacz ile równe jest 2r
To z tego wyznacz ile równe jest 2r 
 c= a−r+b−r ⇒ 2r= a+b−c
c= a−r+b−r ⇒ 2r= a+b−c

 Zresztą ja nie mam takiego zacięcia co Ty Etuś w 'produkowaniu się'
Zresztą ja nie mam takiego zacięcia co Ty Etuś w 'produkowaniu się'  Ja jednak leniuch jestem
Ja jednak leniuch jestem
