Znajdź elementy wyróżnione zbiorów asdf: Znajdź elementy wyróżnione zbiorów: W zbiorze C = C \ {iy : y ∈ R} określona jest relacja R w następujący sposób: z R z' ⇔ Re(z) = Re(z') ∧ arg(z) > arg(z'). B = {z ∊ C : |z| ≤ 3} Wyznaczyć: kres górny kres dolny minoranty majoranty elementy maksymalne elementy minimalne elementy największe elementy najmniejsze Jak to zrobić?

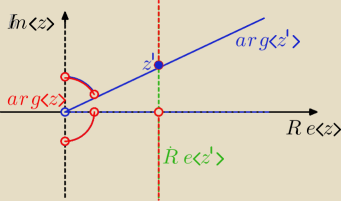
iteRacj@: Nie będę rozwiązywać tego zadania, ale mam prośbę o sprawdzenie, czy dobrze zaznaczyłam podane w nim warunki. C \ {iy : y ∈ R} to płaszczyzna zespolona bez osi Im(z) ? czy w relacji R z liczbą z' pozostają liczby z należące do przerywanych półprostych bez początku?

iteRacj@: błąd, wpis bez sensu bo zaczęłam od z'

asdf: C \ {iy : y ∈ R} to płaszczyzna zespolona bez osi Im(z) ? Też tak uważam Jednak co do rysunku nie mam pewności

iteRacj@: rysunek jest błędny

Pytający: Jak należy interpretować arg(z)?

Rivit: Argument liczby zespolonej – miara kąta skierowanego między wektorem reprezentującym liczbę zespoloną na płaszczyźnie zespolonej, a osią rzeczywistą. Tak mowi Wikipedia Rysunek jest błędny ale to nie zmienia faktu że to zbiór zespolonych bez osi Im(z)