Witam,
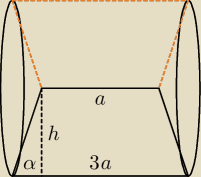
Trapez o podstawach długości a i 3a oraz ostrym kącie α obraca się wokół krótszej podstawy.
Obliczyć objętość bryły.
| h | ||
tg(α) = | ||
| a |
| 1 | 1 | π(tg(α)a)2*a | πa3 tg2(α) | |||||
Vstożka = | Pp*H = | πr2H = | = | |||||
| 3 | 3 | 3 | 3 |
| πa3 tg2(α) | ||
Vbryły = Vwalca − 2Vstożka = 3πa3 tg2(α) − 2 | = ... | |
| 3 |
| 2x | 9x | 2x | 7x | 7πa3 tg2(α) | ||||||
... = 3x − | = | − | = | = | ||||||
| 3 | 3 | 3 | 3 | 9 |
| 5^2 | 52 |
| 2^{10} | 210 |
| a_2 | a2 |
| a_{25} | a25 |
| p{2} | √2 |
| p{81} | √81 |
| Kliknij po więcej przykładów | |
|---|---|
| Twój nick | |